-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
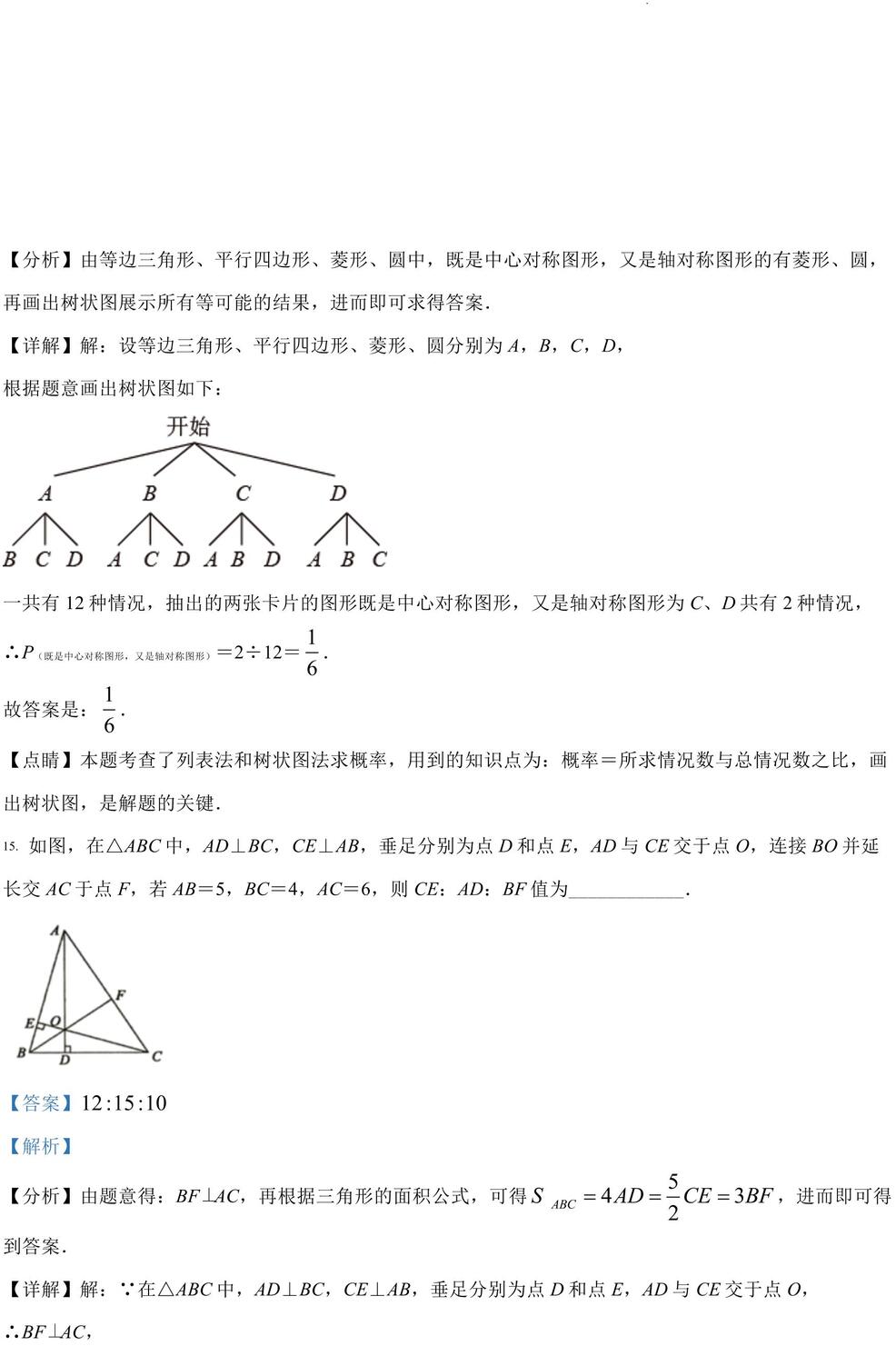
【分析】由等边三角形、平行四边形、菱形、圆中，既是中心对称图形，又是轴对称图形的有菱形、圆，再画出树状图展示所有等可能的结果，进而即可求得答案．
【详解】解：设等边三角形、平行四边形、菱形、圆分别为 A，B，C，D， 根据题意画出树状图如下： 一共有 12 种情况，抽出的两张卡片的图形既是中心对称图形，又是轴对称图形为 C、D 共有 2 种情况，
∴P（既是中心对称图形，又是轴对称图形）＝2÷12＝故答案是：
【点睛】本题考查了列表法和树状图法求概率，用到的知识点为：概率＝所求情况数与总情况数之比，画出树状图，是解题的关键．
15. 如图，在△ABC 中，AD⊥BC，CE⊥AB，垂足分别为点 D 和点 E，AD 与 CE 交于点 O，连接 BO 并延长交 AC 于点 F，若 AB＝5，BC＝4，AC＝6，则 CE：AD：BF 值为____________．
【答案】12 :15 :10
【分析】由题意得：BF⊥AC，再根据三角形的面积公式，可得
S AD CE BF= = = ，进而即可得到答案．
【详解】解：∵在△ABC 中，AD⊥BC，CE⊥AB，垂足分别为点 D 和点 E，AD 与 CE 交于点 O，