-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
（3）从上表中选择合适 统计量，说明哪个班的成绩更均匀．
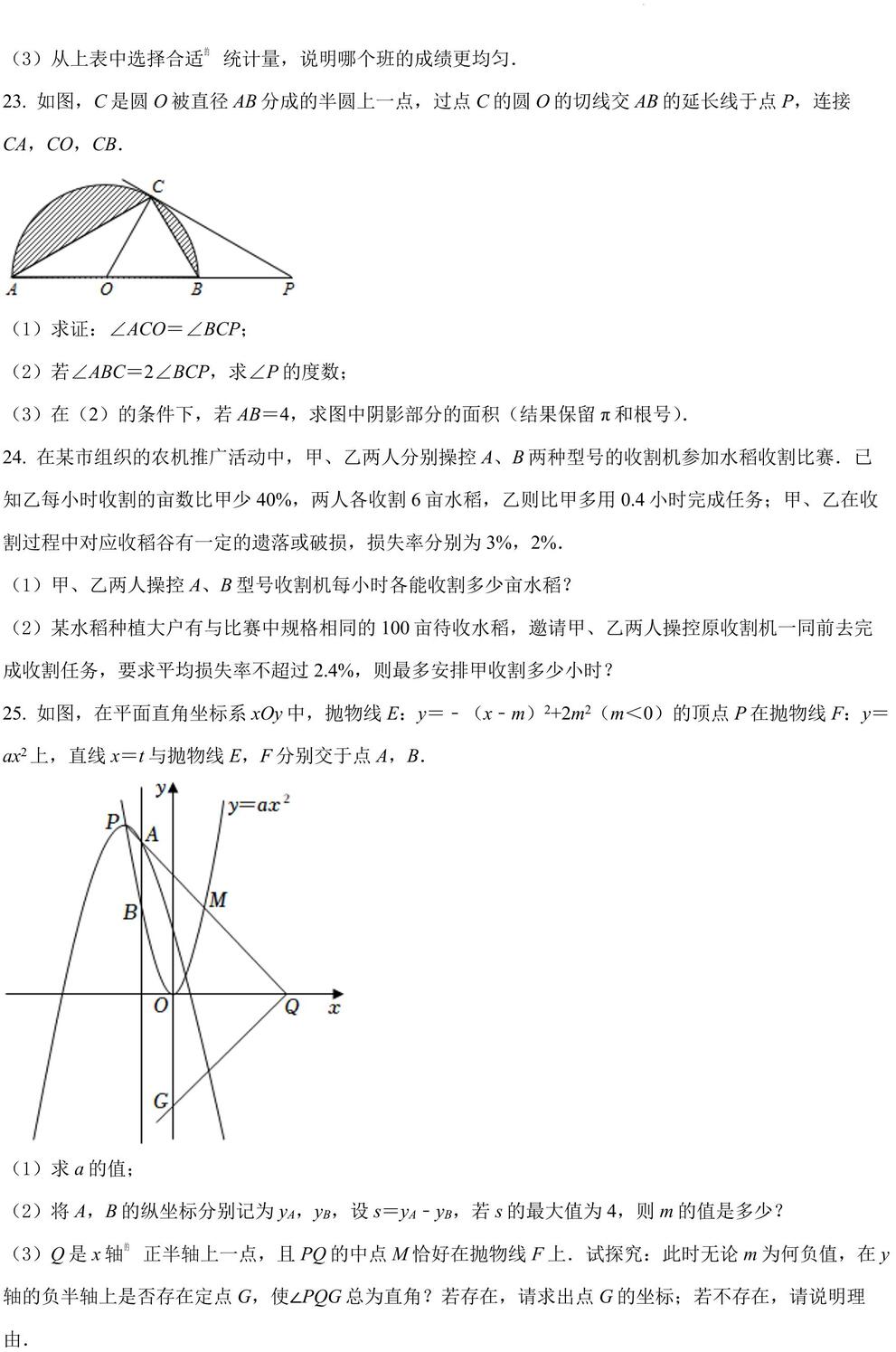
23. 如图，C 是圆 O被直径 AB 分成的半圆上一点，过点 C 的圆 O 的切线交 AB 的延长线于点 P，连接
（1）求证：∠ACO＝∠BCP；
（2）若∠ABC＝2∠BCP，求∠P 的度数；
（3）在（2）的条件下，若 AB＝4，求图中阴影部分的面积（结果保留 π和根号）．
24. 在某市组织的农机推广活动中，甲、乙两人分别操控 A、B 两种型号的收割机参加水稻收割比赛．已知乙每小时收割的亩数比甲少 40%，两人各收割 6亩水稻，乙则比甲多用 0.4 小时完成任务；甲、乙在收割过程中对应收稻谷有一定的遗落或破损，损失率分别为 3%，2%．
（1）甲、乙两人操控 A、B型号收割机每小时各能收割多少亩水稻？
（2）某水稻种植大户有与比赛中规格相同的 100亩待收水稻，邀请甲、乙两人操控原收割机一同前去完成收割任务，要求平均损失率不超过 2.4%，则最多安排甲收割多少小时？
25. 如图，在平面直角坐标系 xOy 中，抛物线 E：y＝﹣（x﹣m）2+2m2（m＜0）的顶点 P 在抛物线 F：y＝
ax2上，直线 x＝t 与抛物线 E，F 分别交于点 A，B．
（1）求 a 的值；
（2）将 A，B 的纵坐标分别记为 yA，yB，设 s＝yA﹣yB，若 s 的最大值为 4，则 m 的值是多少？
（3）Q 是 x轴 正半轴上一点，且 PQ 的中点 M恰好在抛物线 F 上．试探究：此时无论 m 为何负值，在 y轴的负半轴上是否存在定点 G，使∠PQG总为直角？若存在，请求出点 G 的坐标；若不存在，请说明理由．