-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
，即 ． 解得 ．
【点睛】本题属于二次函数综合题，涉及待定系数法求函数解析式，二次函数的性质，相似三角形的性质与判定，中点坐标公式等知识，解题的关键是构造相似三角形得出方程进行求解．
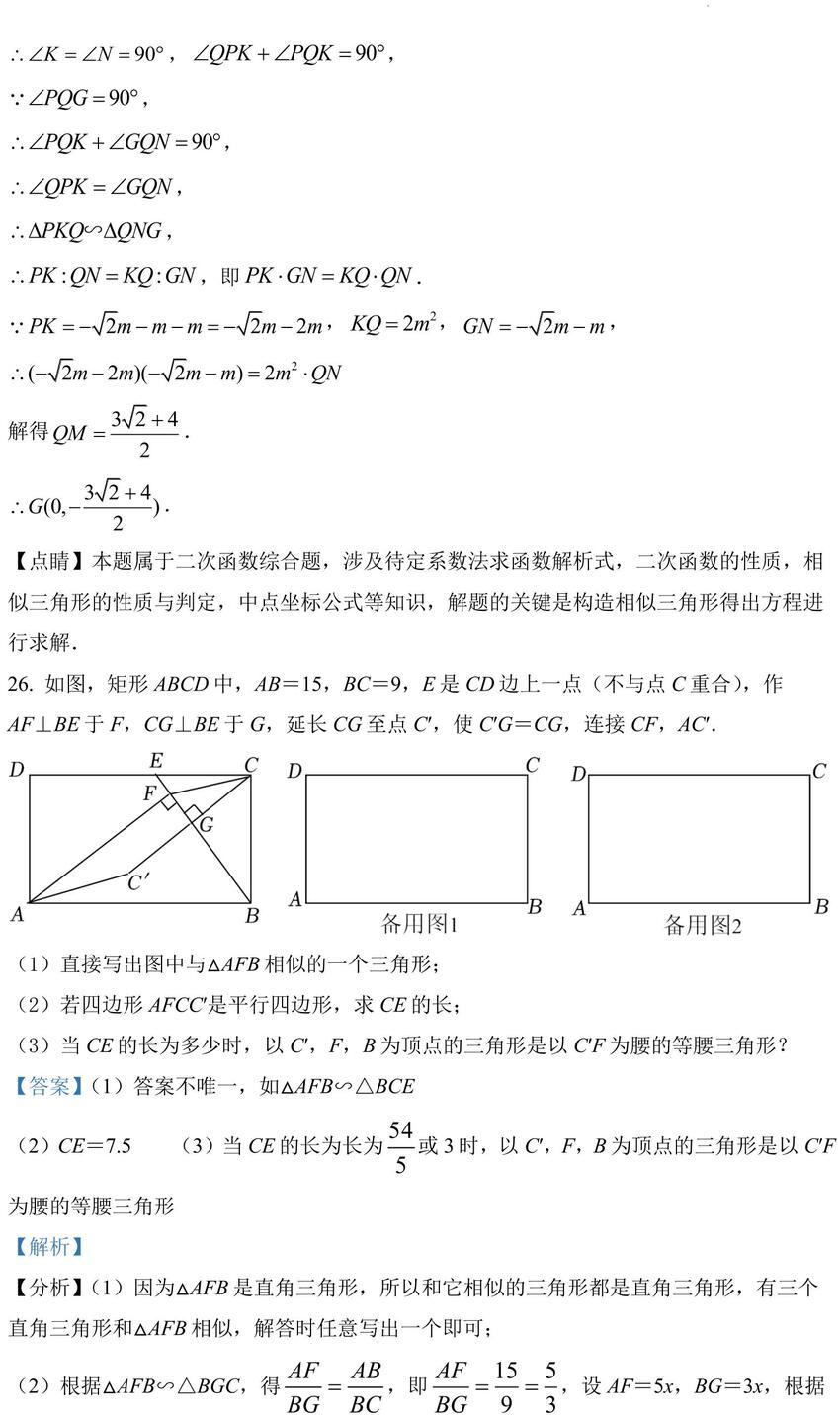
26. 如图，矩形 ABCD 中，AB＝15，BC＝9，E 是 CD 边上一点（不与点 C重合），作
AF⊥BE 于 F，CG⊥BE 于 G，延长 CG至点 C′，使 C′G＝CG，连接 CF，AC′．
（1）直接写出图中与△AFB 相似的一个三角形；
（2）若四边形 AFCC′是平行四边形，求 CE 的长；
（3）当 CE 的长为多少时，以 C′，F，B 为顶点的三角形是以 C′F 为腰的等腰三角形？
【答案】（1）答案不唯一，如△AFB∽△BCE
（2）CE＝7.5 （3）当 CE 的长为长为 或 3 时，以 C′，F，B 为顶点的三角形是以 C′F为腰的等腰三角形
【分析】（1）因为△AFB 是直角三角形，所以和它相似的三角形都是直角三角形，有三个直角三角形和△AFB 相似，解答时任意写出一个即可；
（2）根据△AFB∽△BGC，得 ，即 ，设 AF＝5x，BG＝3x，根据