-
关注“蜜蜂引路”，分配平台账号.
高考题1984年全国统考( )
画出极坐标方程(ρ-2)(θ-π/4)=0(ρ>0)的曲线.
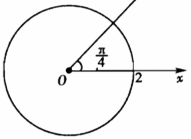
高考题1983年全国统考( )
在极坐标系内，方程ρ=5cosθ表示什么曲线？画出它的图形.
曲线名称是：圆.图形如图所示.
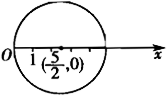
高考题1982年全国统考( )
如图：已知锐角∠AOB=2α内有动点P，PM⊥OA，PN⊥OB，且四边形PMON的面积等于常数c2.今以∠AOB的角平分线OX为极轴，求动点P的轨迹的极坐标方程，并说明它表示 什么曲线.
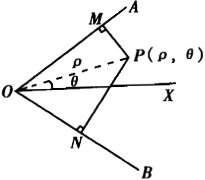
设P点的极坐标为o(ρ,θ),
则 ∠POM=α-θ,∠NOP=α+θ,
OM=ρ cos(α-θ),PM=ρ sin(α-θ),
OM=ρ cos(α+θ),PM=ρ sin(α+θ),
四边形PMON的面积
S=1/2 OM∙PM+1/2 ON∙PN
=ρ2/2[cos(α-θ)sin(α-θ)+cos(α+θ)sin(α+θ)].
依题意，动点P的轨迹的极坐标方程是：
ρ2/2 [cos(α-θ)sin(α-θ)+cos(α+θ)sin(α+θ)]=c2.
用倍角公式化简得ρ2/4 [sin2(α-θ)+sin2(α+θ)]=c2
用和、差公式或和差化积公式化简得
ρ2/2 sin2αcos2θ=c2 即 ρ2 cos2θ=2c2/sin2α.
再化为x2-y2=2c2/sin2α
这个方程表示双曲线.根据题意，动点P的轨迹是双曲线右面一支在∠AOB内的一部分.
高考题2020年全国Ⅲ(文)( )
在直角坐标系 xOy 中, 曲线 C 的参数方程为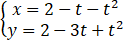
(t 为参数且 t ≠ 1), C 与坐标轴交于 A, B 两点.
(1) 求 |AB|;
(2) 以坐标原点为极点, x 轴正半轴为极轴建立极坐标系, 求直线 AB 的极坐标方程.
(1) 因为 t≠1, 由 2 − t − t2 = 0 得 t = −2, 所以 C 与 y 轴的交点为 (0, 12); 由 2 − 3t + t2 = 0 得 t = 2,
所以 C 与 x 轴的交点为 (−4, 0). 故 |AB| = 4
.
(2) 由 (1) 可知, 直线 AB 的直角坐标方程为 x/(-4)+ y/12 = 1, 将 x = ρcosθ, y = ρsinθ 代入, 得直线 AB 的极坐标方程 3ρcosθ − ρsinθ + 12 = 0.
高考题2020年全国Ⅱ( )
已知 C1, C2 的参数方程分别为 C1 :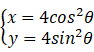
(θ为参数)， C2 : 
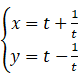(t 为参数) ,
(1) 将 C1, C2 的参数方程化为普通方程;
(2) 以坐标原点为极点, x 轴正半轴为极轴建立极坐标系, 设 C1, C2 的交点为 P , 求圆心在极轴上, 且经过极点和 P 的圆的极坐标方程.
(1) C1 的普通方程为 x + y = 4(0 ⩽ x ⩽ 4).
由 C2 的参数方程得 x2 = t2 + 1/t2 + 2, y2 = t2 + 1/t2 − 2, 所以 x2 − y2 = 4. 故 C2 的普通方程为 x2 − y2 = 4.
(2) 由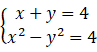
得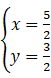 
.
所以 P 的直角坐标为 (5/2 , 3/2).
设所求圆的圆心的直角坐标为(x0, 0), 由题意得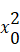 
= (x0-5/2)2 + 9/4, 解得 x0 =17/10.
因此，所求圆的极坐标方程为 ρ = 17/5cos θ.