高考题1984年全国统考( )
设p≠0,实系数一元二次方程z2-2pz+q=0有两个虚数根z1,z2.再设z1,z2在复平面内的对应点是Z1,Z2.求以Z1,Z2为焦点且经过原点的椭圆的长轴的长.
因为p,q为实数,p≠0,z_1,z_2为虚数,所以(-2p)2-4q<0,q>p2>0.
由z1,z2为共轭虚数,知z1,z2关于x轴对称,
所以椭圆短轴在x轴上.
又由椭圆经过原点,可知原点为椭圆短轴的一个端点.
根据椭圆的性质,复数加、减法几何意义及一元二次方程与系数的关系,可得椭圆的
短轴长=2b=|z1 + z2 |=|2p|=2|p|,
焦距=2c=|z1 - z2 | = 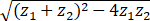 =2
=2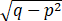 ,
,
长轴长=2a=2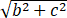 =2
=2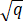 .
.
高考题1983年全国统考( )
当实数t取什么值时,复数z=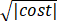 +
+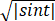 i的辐角主值θ适合0≤θ≤π/4 ?
i的辐角主值θ适合0≤θ≤π/4 ?
因为复数z=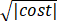 +
+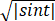 i的实部与虚部都是非负数,所以z的辐角主值θ一定适合0≤θ≤π/2.
i的实部与虚部都是非负数,所以z的辐角主值θ一定适合0≤θ≤π/2.
从而0≤θ≤π/4⇔0≤tanθ≤1.
显然 r=|z|≠0.
因为tanθ=sinθ/cosθ=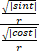 =
= =
=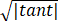 ,
,
所以0≤tanθ≤1⇔0≤√(|tant| )≤1⇔0≤|tant|≤1⇔-1≤tant≤1.
由于y=tant在-π/2<t<π/2内是增函数,并且它的周期是π,因此-1≤tant≤1的解是
kπ-π/4≤t≤kπ+π/4(k为任意整数).
高考题1983年全国统考( )
证明:对于任意实数t,复数z= +
+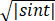 i的模r=|z|适合r≤
i的模r=|z|适合r≤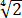 .
.
复数z= +
+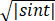 i的模r=|z|为
i的模r=|z|为
r=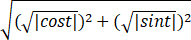
=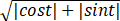 .
.
要对任意实数t,有r≤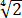 ,只要证对任意实数t,|cost|+|sint|≤
,只要证对任意实数t,|cost|+|sint|≤ 成立.
成立.
对任意实数t,因为|cost|2+|sint|2=1,
所以可令cosφ=|cost|,sinφ=|sint|,
于是|cost|+|sint|=cosφ+sinφ
= (
( /2 cosφ+
/2 cosφ+ /2 sinφ)
/2 sinφ)
= sin(π/4+φ)≤
sin(π/4+φ)≤ ∙1=
∙1= .
.
高考题2020年江苏省( )
已知 i 是虚数单位, 则复数 z = (1 + i)(2 − i) 的实部是______.
3
高考题2020年浙江省( )
已知 a ∈ R, 若 a − 1 + (a − 2)i (i 为虚数单位) 是实数, 则 a =【 】
A、1
B、-1
C、2
D、-2

