高考题1983年全国统考( )
已知y=e-xsin2x,求微分dy.
dy=(e-xsin2x)'dx
=[e-x(sin2x)'+(e-x)'sin2x]dx
=[e-xcos2x(2x)'+e-x(-x)'sin2x]dx
=(2e-xcos2x-e-xsin2x)dx
=e-x(2cos2x-sin2x)dx.
高考题1980年全国统考( )
设直线(l)的参数方程是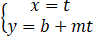 (t是参数)
(t是参数)
椭圆(E)的参数方程是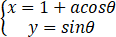 (θ是参数)
(θ是参数)
问:a,b应满足什么条件,使得对于任意m值来说,直线(l)与椭圆(E)总有公共点?
消去参数,得
(l):y=mx+b;(E):(x-1)2/a2 +y2=1.
消去y,整理得(1+a2 m2)x2+2(a2 mb-1)x+a2 b2-a2+1=0.
(l),(E)有交点的条件是上式的判别式≥0,
即(a2 mb-1)2-(1+a2 m2)(a2 b2-a2+1)≥0.
化简并约去a2得
(a2-1)m2-2bm+(1-b2)≥0.
对任何m值,要使这个式子永远成立,条件是
(I)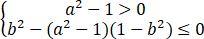 或 (Ⅱ)
或 (Ⅱ)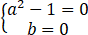
或(I) (Ⅱ)合写成:
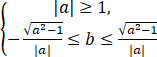
即为所求的条件.
高考题2020年江苏省( )
已知关于 x 的函数 y = f(x), y = g(x) 与 h(x) = kx + b (k, b ∈ R) 在区间 D 上恒有 f(x) ⩾ h(x) ⩾ g(x).
(1) 若 f(x) = x2 + 2x, g(x) = −x2 + 2x, D = (−∞, +∞), 求 h(x) 的表达式;
(2) 若 f(x) = x2 − x + 1, g(x) = k ln x, h(x) = kx − k, D = (0, +∞), 求 k 的取值范围;
(3) 若 f(x) = x4−2x2, g(x) = 4x2−8, h(x) = 4(t3−t)x−3t4+2t2 (0 < |t| ⩽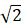 ), D = [m, n] ⊂ [-
), D = [m, n] ⊂ [-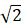 ,
, 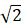 ].
].
求证: n − m ⩽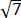 .
.
(1) 由 f(x)=g(x) 得 x=0. 又f' (x)=2x+2,g' (x)=-2x+2, 所以 f' (0)=g' (0)=2.
所以, 函数 h(x) 的图像为过原点, 斜率为 2 的直线, 所以 h(x)=2x. 经检验, h(x)=2x 符合题意.
(2) h(x)-g(x)=k(x-1-lnx).
设 φ(x)=x-1-lnx, 则 φ' (x)=1-1/x=(x-1)/x; φ(x)≥φ(1)=0. 所以当 h(x)-g(x)≥0 时, k≥0.
由f(x)-h(x)=x2-x+1-(kx-k)=x2-(k+1)x+(1+k)≥0,得:
当 x=k+1≤0 时, f(x) 在 (0,+∞) 上递增, 所以 f(x)=1+k≥0, 所以k=-1.
当 k+1>0 时, ∆≤0, 即 (k+1)2-4(k+1)≤0,(k+1)(k-3)≤0,-1<k≤3.
综上, k ∈ [0, 3] .
(3) 因为 f(x)=x4-2x2, 所以 f' (x)=4x3-4x=4x(x+1)(x-1).所以函数 y=f(x) 的图像在 x=x0 处的切线为
y=(4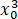 -4x0 )(x-x_0 )+(
-4x0 )(x-x_0 )+(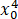 -2
-2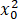 )=(4
)=(4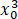 -x0 )x-3
-x0 )x-3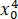 +2
+2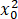 .
.
可见直线 y=h(x) 为函数 y=f(x) 的图像在 x=t (0<|t|≤√2)处的切线. 又因为

由函数 y=h(x) 的图像可知, 当 f(x)≥h(x) 在区间 D 上恒成立时, |t|∈[1,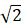 ]
]
又由 g(x)-h(x)=0 得 4x2-4(t3-t)x+3t4-2t2-8=0.
设方程 g(x)-h(x)=0 的两根为 x1, x2, 则x1+x2=t3-t, x1 x2=(3t4-2t2-8)/4,所以
|x1-x2 |=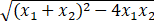 =
=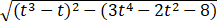 =
=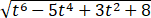 .
.
令 t2=λ, 则 λ∈[1,2], 由图像可知n-m=|x1-x2 |=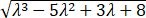 .
.
设 φ(λ)=λ3-5λ2+3λ+8, 则 φ'(λ)=3λ2-10λ+3. 所以当 λ∈[1,2] 时, φ' (λ)<0, φ(λ)单调递减, 所以 φ(λ)max=φ(1)=7. 故 (n-m)max=|x1-x2 |max=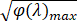 =
=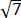 ,即n-m≤
,即n-m≤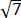 .
.
高考题2020年江苏省( )
某地准备在山谷中建一座桥梁, 桥址位置的竖直截面图如图所示: 谷底 O 在水平线 MN 上, 桥 AB 与 MN平行, OO′为铅垂线 (O′在 AB 上), 经测量, 左侧曲线 AO 上任一点 D 到 MN 的距离 h1 (米) 与 D 到 OO′ 的距离 a (米) 之间满足关式 h1=1/40 a2 ; 右侧曲线 BO 上任一点 F 到 MN 的距离 h2 (米) 与 F 到 OO′的距离 b (米)之间满足关系式 h2=-1/800 b3+6b . 已知点 B 到 OO′的距离为 40 米.

(1) 求桥 AB 的长度;
(2) 计划在谷底两侧建造平行于 OO′的桥墩 CD 和 EF , CE 为 80 米, 其中 C, E 在 AB 上 (不包括端点), 桥墩 EF 每米造价 k (万元), 桥墩 CD 每米造价 3/2 k (万元) (k > 0), 问 O′E为多少米时, 桥墩 CD 与 EF 的总造价最低?
(1) 过 A, B 分别作 MN 的垂线, 垂足为 A′, B′, 则 AA′ = BB′ = AA'=BB'=-1/800×403+6×40=160 .
令 1/40 a2=160 , 得 a = 80, 所以 AO′= 80, AB = AO′+ BO′= 80 + 40 = 120.
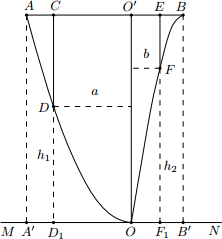
(2) 设 O′E = x, 则 CO′= 80 − x, 由 ,得 0<x<40.
,得 0<x<40.
总造价 y=3k/2 [160-1/40 (80-x)2 ]+k[160-(-1/800 x3+6x)]=k/800(x3-30x2+160×800) , 则
y'=k/800 (3x2-60x)=3k/800 x(x-20) .
因为 k > 0, 所以令 y′= 0, 得 x = 0 或 20, 所以当 0 < x < 20 时, y′< 0, y 单调递减; 当 20 < x < 40 时,
y′> 0, y 单调递增. 所以, 当 x = 20 时, y 取最小值, 造价最低.
高考题2020年浙江省( )
已知 1 < a ⩽ 2, 函数 f(x) = ex − x − a, 其中 e = 2.71828 … 为自然对数的底数.
(I) 证明: 函数 y = f(x) 在 (0, +∞) 上有唯一零点;
(II) 记 x0 为函数 y = f(x) 在 (0, +∞) 上的零点, 证明:
(i) 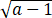 ≤x0≤
≤x0≤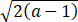 ;
;
(ii) x0 f(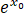 )≥(e-1)(a-1)a .
)≥(e-1)(a-1)a .
(I) 因为 f(0) = 1 − a < 0, f(2) = e2 − 2 − a ⩾ e2 − 4 > 0, 所以 y = f(x) 在 (0, +∞) 上存在零点.
因为 f′(x) = ex − 1, 所以当 x > 0 时, f′(x) > 0, 故函数 f(x) 在 (0, +∞) 上单调递增.
所以函数 y = f(x) 在 (0, +∞) 上有唯一零点.
(II) (i) 令 g(x)=ex-1/2 x2-x-1 (x ⩾ 0), 则 g' (x)=ex-x-1=f(x)+a-1 .
由 (i) 知函数 g′(x) 在[0, +∞)上单调递增, 故当 x > 0 时, g′(x) > g′(0) = 0.
所以函数 g(x) 在 [0, +∞) 单调递增, 故 g(x) ⩾ g(0) = 0. 由 g(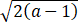 )≥0得
)≥0得
f(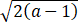 )=
)=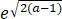 -
-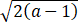 -a≥0=f(x0)
-a≥0=f(x0)
因为 f(x) 在 [0, +∞) 单调递增, 故 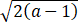 ≥x0.
≥x0.
令 h(x) = ex − x2 − x − 1 (0 ⩽ x ⩽ 1), 则 h′(x) = ex − 2x − 1.
令 h1(x) = ex − 2x − 1 (0 ⩽ x ⩽ 1), 则h1' (x)=ex-2, 所以

故当 0 < x < 1 时, h1(x) < 0 , 即 h′(x) < 0, 所以 h(x) 在 [0, 1] 单调递减.
因此当 0 ⩽ x ⩽ 1 时, h(x) ⩽ h(0) = 0. 由 h(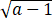 )≤0 得
)≤0 得
f(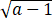 )=
)=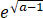 -
-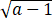 -a≤0=f(x0)
-a≤0=f(x0)
因为 f(x) 在 [0, +∞] 单调递增, 故 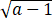 ≤x0.
≤x0.
综上, 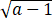 ≤x_0≤
≤x_0≤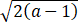 .
.
(ii) 令 u(x) = ex − (e − 1)x − 1, u′(x) = ex − (e − 1), 所以当 x > 1 时, u′(x) > 0.
故函数 u(x) 在区间 [1, +∞] 上单调递增, 因此 u(x) ⩾ u(1) = 0.
由 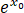 =x0+a 可得
=x0+a 可得
x0 f(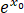 )=x0 f(x0+a)=(ea-1)
)=x0 f(x0+a)=(ea-1) 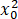 +a(ea-2)x0≥(e-1)a
+a(ea-2)x0≥(e-1)a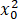
由 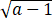 ≤x0 得 x0 f(
≤x0 得 x0 f(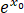 )≥(e-1)(a-1)a.
)≥(e-1)(a-1)a.

