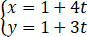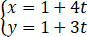-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
高考题2010年上海市( )
直线L的参数方程式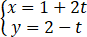
(t∈R)，则 L的方向向量d可以是 【 】
A、(1,2)
B、(2,1)
C、(-2,1)
D、(1,-2)
(-2,1)
高考题1984年全国统考( )
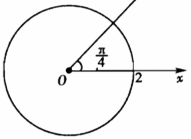
画出极坐标方程(ρ-2)(θ-π/4)=0(ρ>0)的曲线.
高考题1982年全国统考( )
在平面直角坐标系内，下述方程表示什么曲线？画出它的图形.
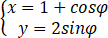
原参数方程化为(x-1)2+y2/4=1，图形是椭圆，作图如下：
高考题1980年全国统考( )
设直线(l)的参数方程是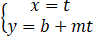
(t是参数)
椭圆(E)的参数方程是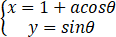
(θ是参数)
问：a,b应满足什么条件，使得对于任意m值来说，直线(l)与椭圆(E)总有公共点？
消去参数，得
(l):y=mx+b；(E):(x-1)2/a2 +y2=1.
消去y，整理得(1+a2 m2)x2+2(a2 mb-1)x+a2 b2-a2+1=0.
(l),(E)有交点的条件是上式的判别式≥0，
即(a2 mb-1)2-(1+a2 m2)(a2 b2-a2+1)≥0.
化简并约去a2得
(a2-1)m2-2bm+(1-b2)≥0.
对任何m值，要使这个式子永远成立，条件是
(I)
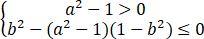或 (Ⅱ)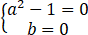
或(I) (Ⅱ)合写成：
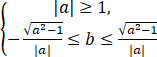
即为所求的条件.
高考题2020年上海市( )
已知直线 l 的解析式为 3x − 4y + 1 = 0, 则下列各式是 l 的参数方程的是【 】
A、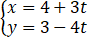
B、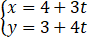
C、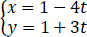
D、