-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
∴直线 A 的解析式为 y=（n-m）x-mn，
∴直线 A 的解析式为 y=（n-m）x+3， 故直线 A 一定过定点（0，3）．
【点睛】本题考查了抛物线与一次函数的交点问题，待定系数法，一元二次方程根与系数关系定理，对称性，熟练掌握抛物线与一次函数的交点，及其根与系数关系定理是解题的关键．
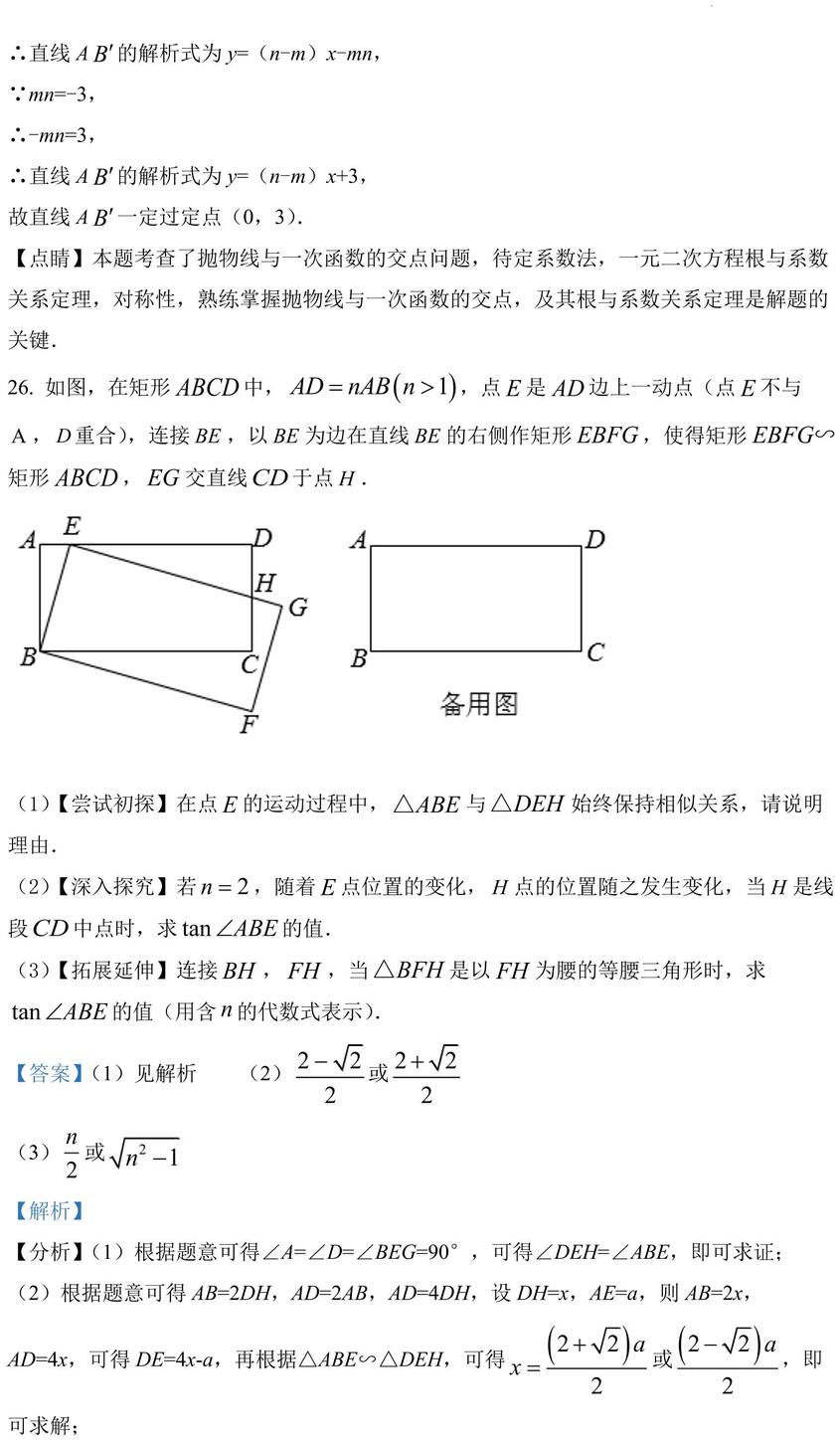
26. 如图，在矩形 中， ，点 是 边上一动点（点 不与
， 重合），连接 ，以 为边在直线 的右侧作矩形 ，使得矩形矩形 ， 交直线 于点 ．
（1）【尝试初探】在点 的运动过程中， 与 始终保持相似关系，请说明理由．
（2）【深入探究】若 ，随着 点位置的变化， 点的位置随之发生变化，当 是线段 中点时，求 的值．
（3）【拓展延伸】连接 ， ，当 是以 为腰的等腰三角形时，求的值（用含 的代数式表示）．
【答案】（1）见解析 （2） 或
（3） 或
【分析】（1）根据题意可得∠A=∠D=∠BEG=90°，可得∠DEH=∠ABE，即可求证；
（2）根据题意可得 AB=2DH，AD=2AB，AD=4DH，设 DH=x，AE=a，则 AB=2x，
AD=4x，可得 DE=4x-a，再根据△ABE∽△DEH，可得 或 ，即可求解；