2022年陕西省初中学业水平考试(中考)数学试卷

【小问 3详解】 令 ， 由 ，得 ，∴ ．（舍去） 由 ，得 ，∴ ．

∴输出的 y 值为 0 时，输入的 x 值为 ．

【点睛】本题主要考查了待定系数法求一次函数关系式，理解“函数求值机”的计算过程是解题的关键．

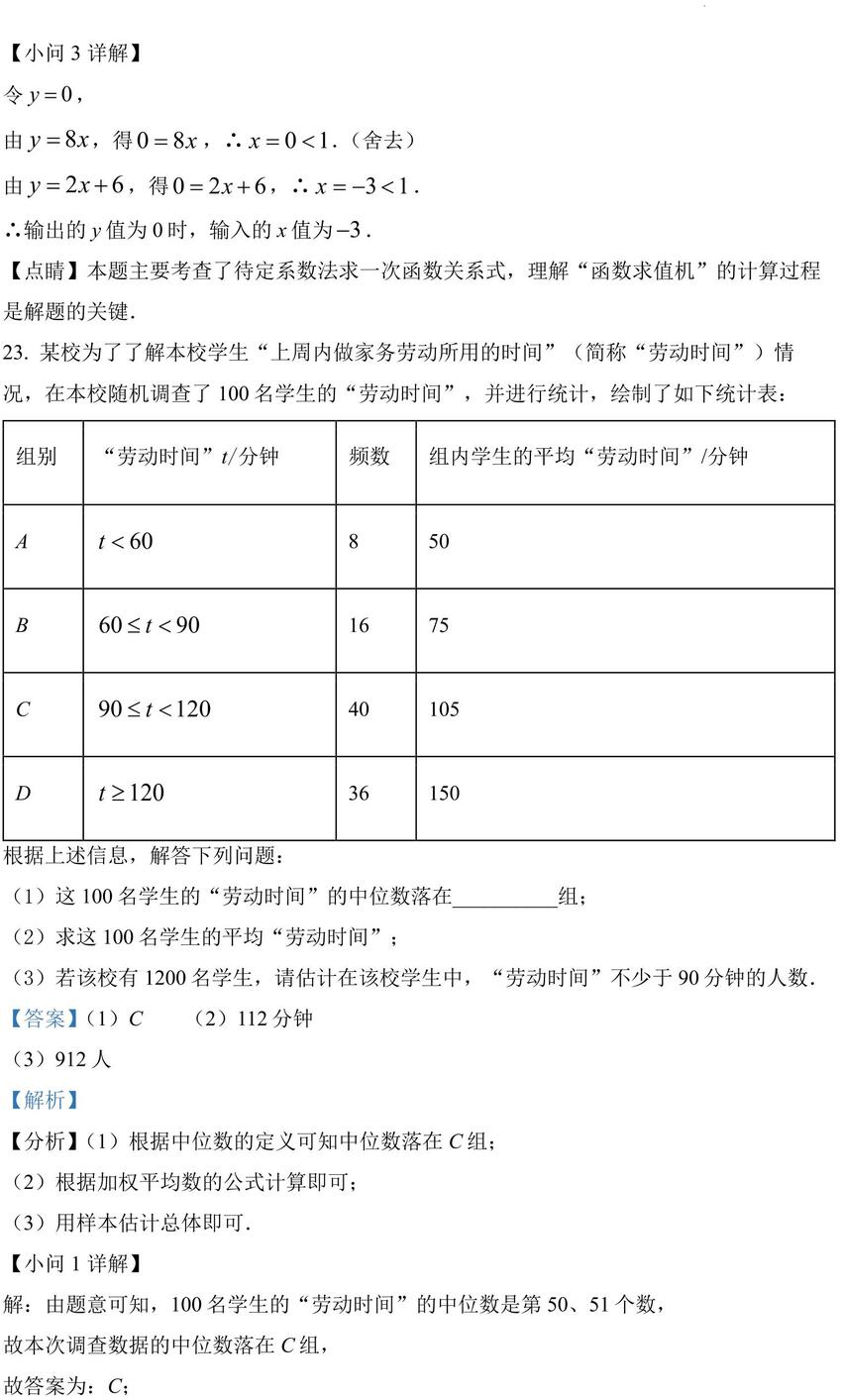
23. 某校为了了解本校学生“上周内做家务劳动所用的时间”（简称“劳动时间”）情况，在本校随机调查了 100 名学生的“劳动时间”，并进行统计，绘制了如下统计表： 组别 “劳动时间”t/分钟 频数 组内学生的平均“劳动时间”/分钟 根据上述信息，解答下列问题：

（1）这 100 名学生的“劳动时间”的中位数落在__________组；

（2）求这 100 名学生的平均“劳动时间”；

（3）若该校有 1200 名学生，请估计在该校学生中，“劳动时间”不少于 90 分钟的人数．

【答案】（1）C （2）112 分钟

（3）912人

【分析】（1）根据中位数的定义可知中位数落在 C 组；

（2）根据加权平均数的公式计算即可；

（3）用样本估计总体即可．

【小问 1详解】 解：由题意可知，100 名学生的“劳动时间”的中位数是第 50、51 个数， 故本次调查数据的中位数落在 C 组， 故答案为：C；