2022年陕西省初中学业水平考试(中考)数学试卷

故选：A．

【点睛】本题主要考查了圆周角定理，根据圆周角定理的出∠AOB=2∠C=92°是解答本题的关键．

8. 已知二次函数 y=x2?2x?3 的自变量 x1，x2，x3对应的函数值分别为 y1，y2，y3．当

?13 时，y1，y2，y3三者之间的大小关系是（ ）

【分析】先求得抛物线的对称轴为直线 x=1，抛物线与 x 轴的交点坐标，画出草图，利用数形结合，即可求解．

【详解】解：y=x2?2x?3=(x-1)2-4，

∴对称轴为直线 x=1， 令 y=0，则(x-1)2-4=0， 解得 x1=-1，x2=3，

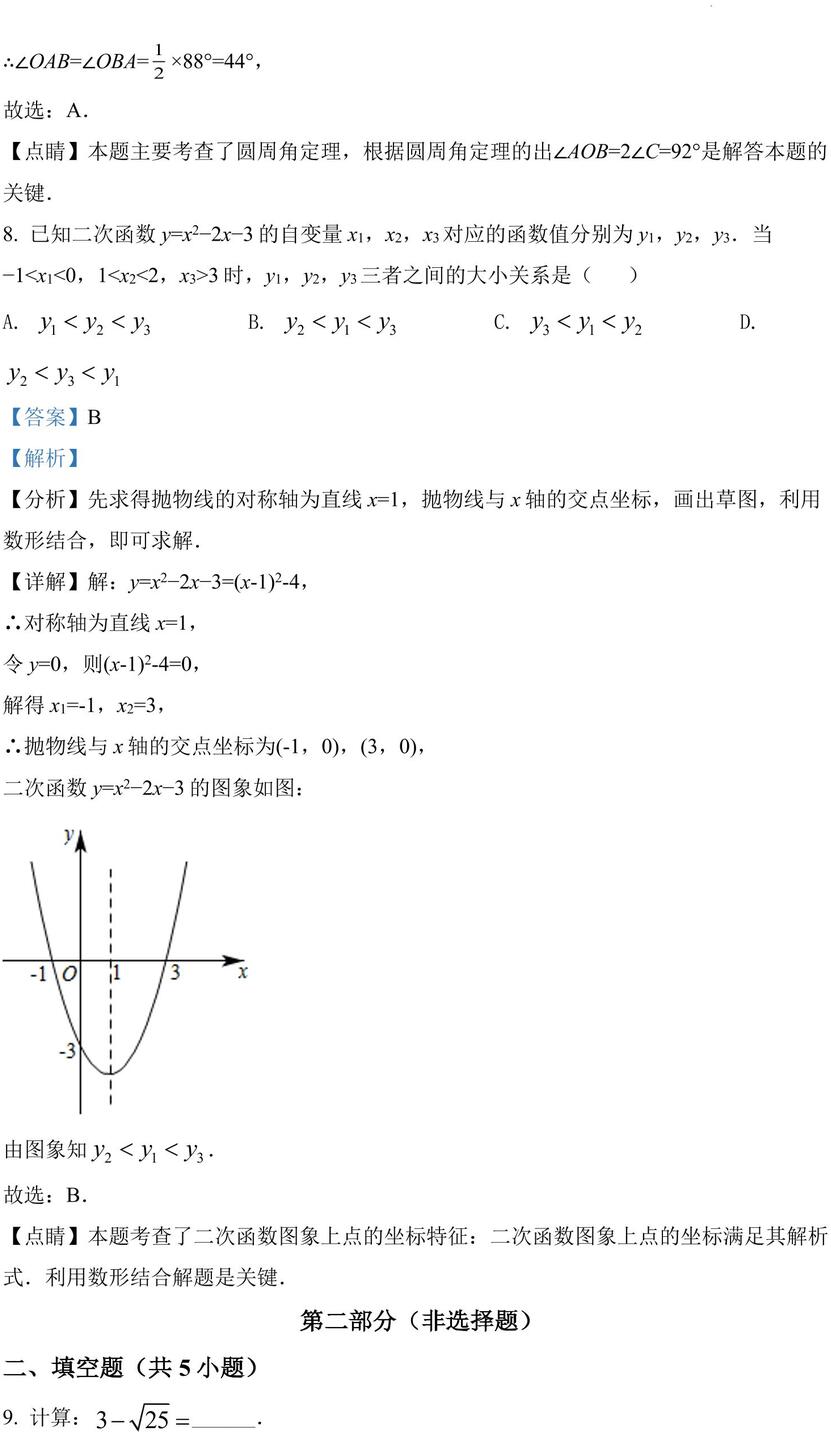
∴抛物线与 x 轴的交点坐标为(-1，0)，(3，0)， 二次函数 y=x2?2x?3 的图象如图： 由图象知 ． 故选：B．

【点睛】本题考查了二次函数图象上点的坐标特征：二次函数图象上点的坐标满足其解析式．利用数形结合解题是关键． 第二部分（非选择题）

二、填空题（共 5小题）

9. 计算： ______．