-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
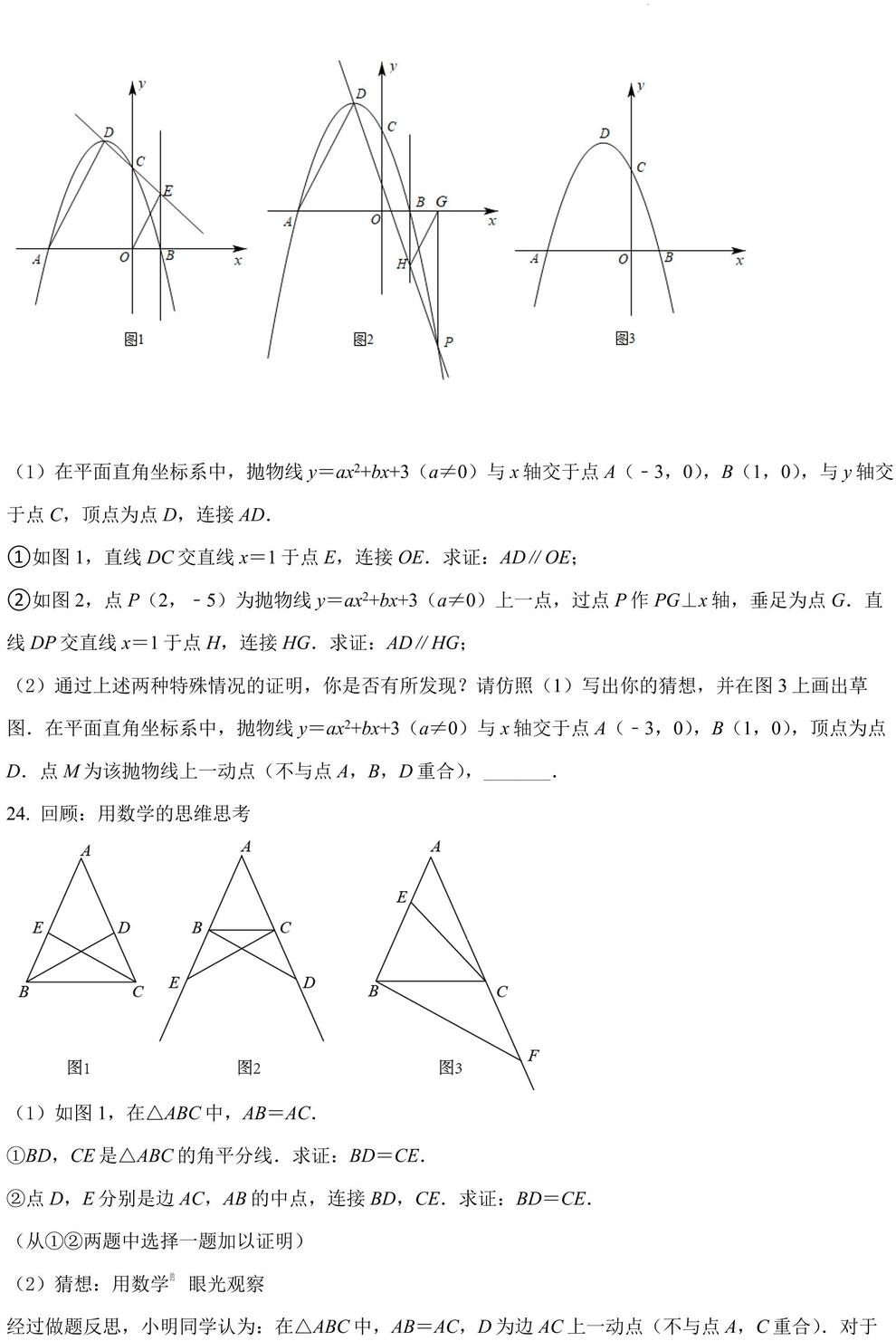
（1）在平面直角坐标系中，抛物线 y＝ax2+bx+3（a≠0）与 x轴交于点 A（﹣3，0），B（1，0），与 y轴交于点 C，顶点为点 D，连接 AD．
①如图 1，直线 DC交直线 x＝1 于点 E，连接 OE．求证：AD∥OE；
②如图 2，点 P（2，﹣5）为抛物线 y＝ax2+bx+3（a≠0）上一点，过点 P 作 PG⊥x轴，垂足为点 G．直线 DP交直线 x＝1 于点 H，连接 HG．求证：AD∥HG；
（2）通过上述两种特殊情况的证明，你是否有所发现？请仿照（1）写出你的猜想，并在图 3 上画出草图．在平面直角坐标系中，抛物线 y＝ax2+bx+3（a≠0）与 x轴交于点 A（﹣3，0），B（1，0），顶点为点
D．点 M 为该抛物线上一动点（不与点 A，B，D重合），_______．
24. 回顾：用数学的思维思考
（1）如图 1，在△ABC 中，AB＝AC．
①BD，CE 是△ABC 的角平分线．求证：BD＝CE．
②点 D，E 分别是边 AC，AB 的中点，连接 BD，CE．求证：BD＝CE．
（从①②两题中选择一题加以证明）
（2）猜想：用数学 眼光观察 经过做题反思，小明同学认为：在△ABC 中，AB＝AC，D 为边 AC 上一动点（不与点 A，C 重合）．对于