-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
【点睛】这是一道关于四边形的综合问题，主要考查了正方形的性质，全等三角形的性质和判定，平行四边形的判定等知识．
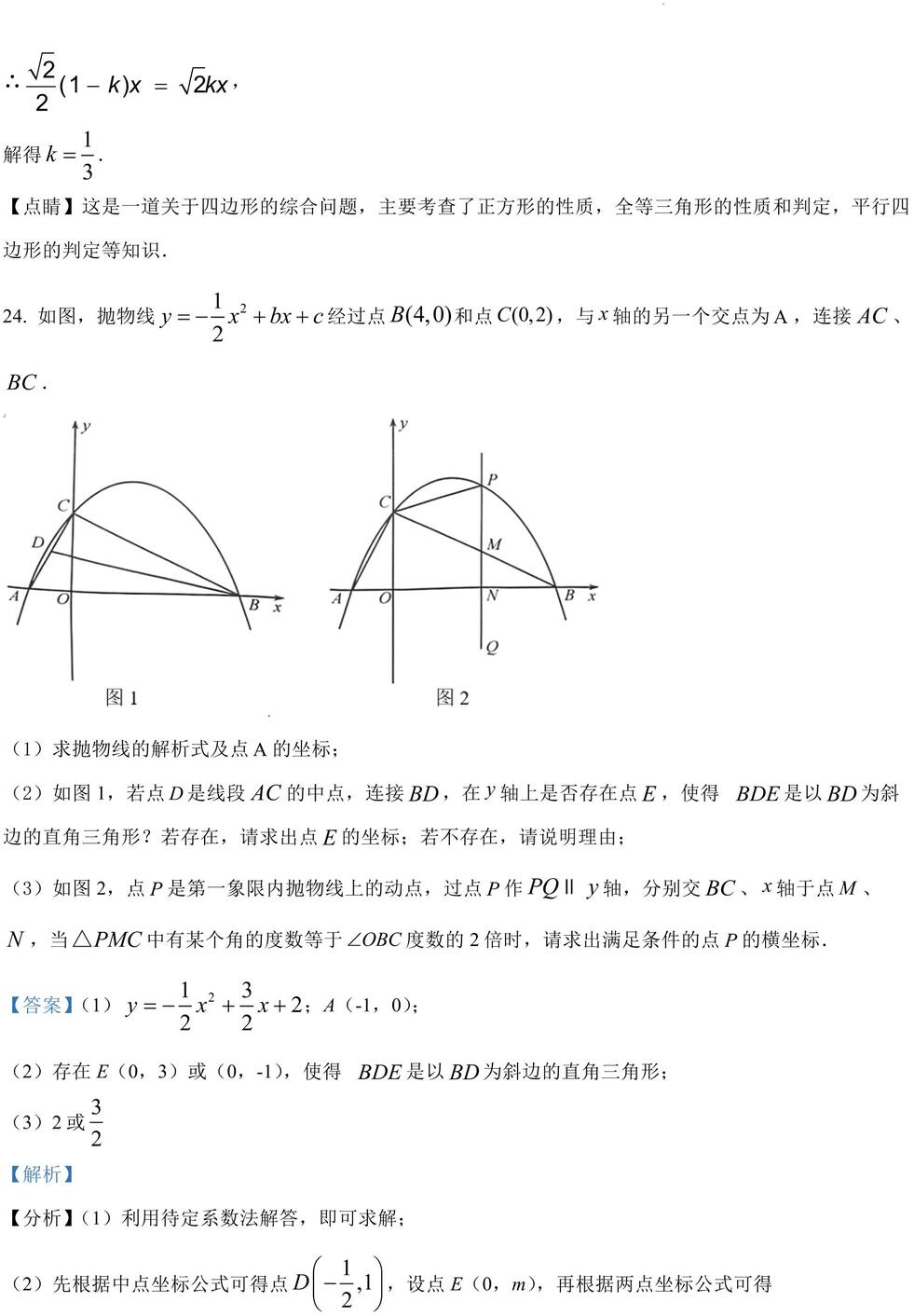
24. 如图，抛物线 2
y x bx c= - + + 经过点 (4,0)B 和点 (0,2)C ，与 x轴的另一个交点为A，连接 AC、
（1）求抛物线的解析式及点A的坐标；
（2）如图 1，若点D是线段 AC的中点，连接 BD，在 y轴上是否存在点 E，使得 BDE是以 BD为斜边的直角三角形？若存在，请求出点 E的坐标；若不存在，请说明理由；
（3）如图 2，点 P是第一象限内抛物线上的动点，过点 P作 PQ y∥ 轴，分别交 BC、 x轴于点M 、
N ，当 PMC△ 中有某个角的度数等于 OBC? 度数的 2 倍时，请求出满足条件的点 P的横坐标．
【答案】（1） 2
（2）存在 E（0，3）或（0，-1），使得 BDE是以 BD为斜边的直角三角形；
（3）2 或
【分析】（1）利用待定系数法解答，即可求解；
（2）先根据中点坐标公式可得点
，设点 E（0，m），再根据两点坐标公式可得