-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
（2）将条形统计图补充完整；
（3）若该校有 1600 名学生，请估计竞赛成绩在良好以上 的学生有多少人？
（4）在本次竞赛中，综治办发现七（1）班、八（4）班的成绩不理想，学校要求这两个班加强学习一段时间后，再由电脑随机从 A、B、C、D 四套试卷中给每班派发一套试卷进行测试，请用列表或画树状图的方法求出两个班同时选中同一套试卷的概率．
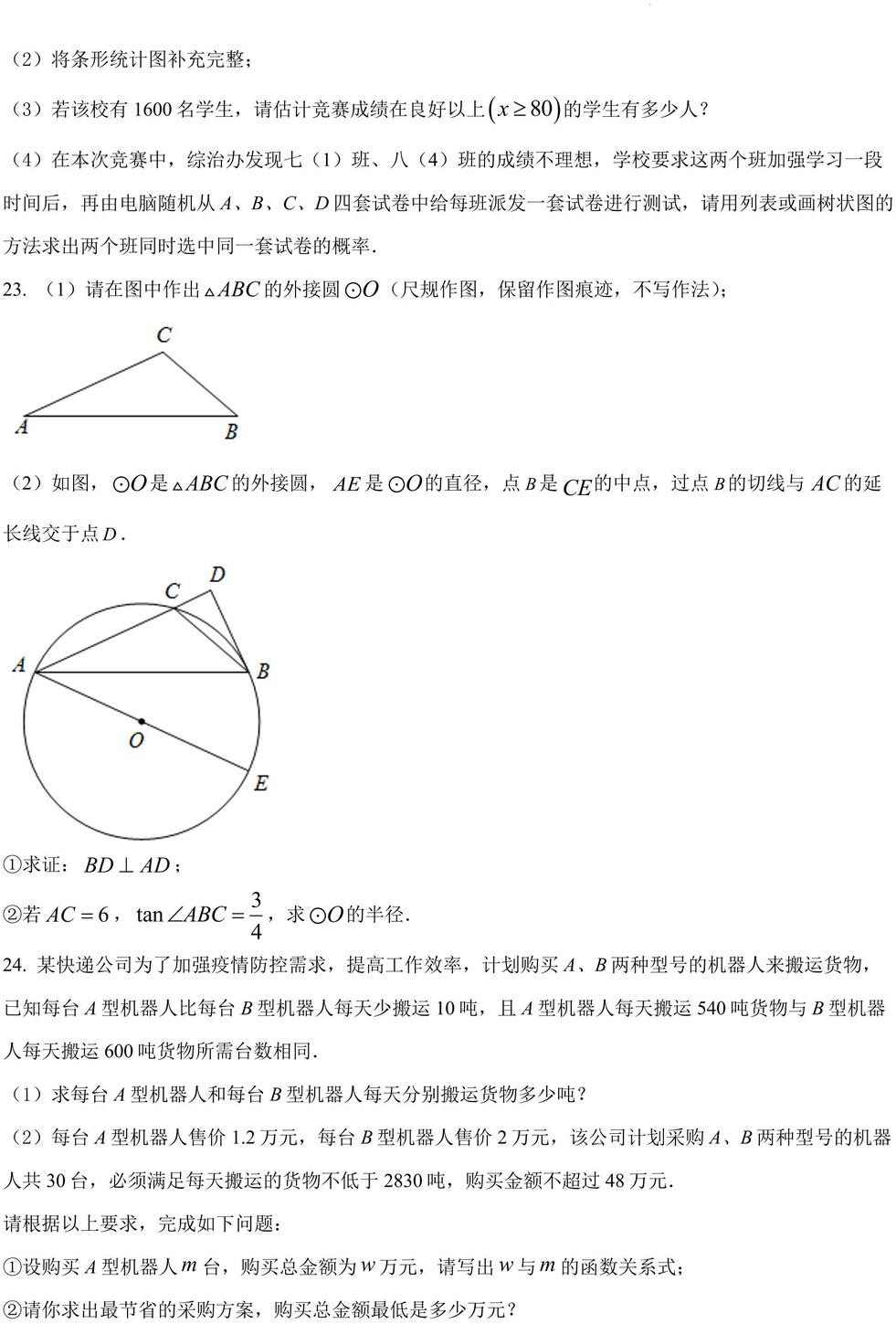
23. （1）请在图中作出 的外接圆 （尺规作图，保留作图痕迹，不写作法）；
（2）如图， 是 的外接圆， 是 的直径，点 是 的中点，过点 的切线与 的延长线交于点 ．
①求证： ；
②若 ， ，求 的半径．
24. 某快递公司为了加强疫情防控需求，提高工作效率，计划购买 A、B 两种型号的机器人来搬运货物，已知每台 A型机器人比每台 B型机器人每天少搬运 10吨，且 A型机器人每天搬运 540吨货物与 B型机器人每天搬运 600吨货物所需台数相同．
（1）求每台 A型机器人和每台 B型机器人每天分别搬运货物多少吨？
（2）每台 A型机器人售价 1.2万元，每台 B型机器人售价 2万元，该公司计划采购 A、B 两种型号的机器人共 30台，必须满足每天搬运的货物不低于 2830吨，购买金额不超过 48万元． 请根据以上要求，完成如下问题：
①设购买 A型机器人 台，购买总金额为 万元，请写出 与 的函数关系式；
②请你求出最节省的采购方案，购买总金额最低是多少万元？