-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
高考题1984年全国统考( )
要排一张有6个歌唱节目和4个舞蹈节目的演出节目单，任何两个舞蹈节目不得相信，问：有多少种不同的排法？（只要写出式子，不必计算）
6!
插空法，先将6个歌唱节目排成一排，有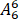
种排法，再从7个空隙中任选4个排舞蹈节目有种排法，故共有不同排法种数
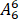
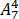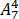=6!
高考题1984年全国统考( )
求(|x|+1/|x| -2)3的展开式中的常数项.
-20
高考题1983年全国统考( )
一个小组共有10名同学，其中4名是女同学，6名是男同学. 要从小组内选出3名代表，其中至少1名女同学，一共有多少种选法？
10外代表中任选3名代表的选法的种数是
=120.
3外代表都是男同学的选法的种数是
=20.
所以3名代表中至少有1名女同学的选法有
- 
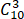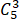=120-20=100(种).
高考题1982年全国统考( )
求(-1+i)20展开式中第15项的数值.
T15=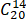
(-1)6 ∙i14
=
=-
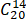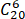
=-38760
高考题1981年全国统考( )
在 A , B , C , D 四位候选人中：
1．如果选举正、副班长各一人，共有几种选法？写出所有可能的选举结果．
2．如果选举班委三人，共有几种选法？写出所有可能的选举结果．
1. 选法种数 
=4×3=12(种).
所有可能的选举结果（把正班长、副班长按次序来写）：AB，AC，AD，BC，BD，CD，BA，CA，DA，CB，DB，DC.
2. 选法种数
=
=4(种).
所有可能的选举结果：ABC，ABD，ACD，BCD.