解 答 题(数学·2025年·广东省)
综合与实践
【阅谈材料】
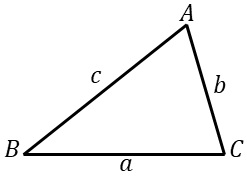
如图,在锐角△ABC中,
∠A,∠B,∠C的对边长分别为a,b,c,则有
a/sinA=b/sinB=c/sinC,这是解三角形的重要结论,可用于解决实际问题.
【问题提出】
万绿湖是广东省重要的生态屏障和饮用水水源地.某综合与实践小组要绘制一幅万绿湖局部平面示意图,现需要知道湖中A,B两岛间的实际距离,由于地形原因,无法利用测距仪直接测量,该小组对这一问进行了探究.
【方案设计】
工具:测角仪、测距仪、无人机(只能测角度、水平面高度)
测角仪 测距仪 无人机
测量过程:
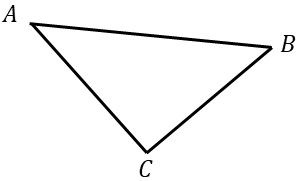
步骤1:如下图,在空旷地找一点C;
步骤2:利用无人机多次测量并取平均值测得∠A≈43°,∠B≈51°;
步骤3:利用测距仪多次测最并取平均值测得BC≈341m,AC≈388.5m.
【问题解决】
⑴请你利用【阅读材料】中的结论计算A,B两岛间的距离.
(参考数据: sin43°≈0.682,sin51°≈0.777,sin86°≈0.998)
【评价反思】
⑵设计共他方案计算A,B两岛间的距离,要求:选用【方案设计】中的工具,写出你的方案和所用的数学知识.
解答提示
解答过程见word版
自新冠肺炎疫情发生以来,全国人民共同抗疫,各地积极普及科学防控知识.下面是科学防控知识的图片,图片上有图案和文字说明,其中的图案是轴对称图形的是【 】
下列几何体都是由4个大小相同的小正方体组成的,其中主视图与左视图相同的几何体是【 】
泰勒斯是古希腊时期的思想家,科学家,哲学家,他最早提出了命题的证明.泰勒斯曾通过测量同一时刻标杆的影长,标杆的高度。金字塔的影长,推算出金字塔的高度。这种测量原理,就是我们所学的【 】
如图是一张长12cm,宽10cm的矩形铁皮,将其剪去两个全等的正方形和两个全等的矩形,剩余部分(阴影部分)可制成底面积24cm2是的有盖的长方体铁盒.则剪去的正方形的边长为cm.
如图,在RtΔABC中,∠ACB=90°,AC=3,BC=4,CD⊥AB,垂足为D,E为BC的中点,AE与CD交于点F,则DF的长为.
如图,四边形OABC是平行四边形,以点O为圆心,OC为半径的⊙O与AB相切于点B,与AO相交于点D,AO的延长线交⊙O于点E,连接EB交OC于点F,求∠C和∠E的度数.

