题吧，智能辅助学习中心
证 明 题（理工数学Ⅰ·2022年·全国统考）
已知二次型f(x1,x2,x3 )=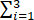
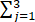ijxixj.
(1)求二次型矩阵.
(2)求正交矩阵Q，使得二次型经正交变换x=Qy化为标准形.
(3)求f(x1,x2,x3)=0的解.
解答提示
(1) f(x1,x2,x3 )=ijxi xj=x12+4x22+9x32+4x1 x2+6x1 x3+12x2 x3，二次型矩阵为A=.(2) |λE-A|==λ2 (λ-14)=0，特征值为λ1=14,λ2=λ3=0.λ1=14时，(λE-A)=0的基础解系为α1=(1,2,3)T;λ2=λ3=0时，(λE-A)=0的基础解系为α2=(-2,1,0)T,α3=(-3,...
查看完整答案，请下载word版
二次型f(x1,x2,x3 ) = (x1 + x2)2 + (x2 + x3)2 - (x3 - x1)2的正惯性指数依次为【 】
设A是n级实对称矩阵，证明rank(A)=n的充要条件是：存在实对称矩阵B使AB+B'A是正定矩阵。
设S1,S3为实对称矩阵，S2为实矩阵，则矩阵S=为正定矩阵的充要条件为矩阵S3与矩阵S1-S2 S3-1 S2'皆为正定矩阵。
设A为实对称矩阵。证明当实数t充分大之后，tI+A是正定矩阵，其中I表示单位矩阵。
设A=(aij)n×n为正定矩阵.证明：f(x1,x2,…,xn )=是负定二次型，其中符号|∙|表示行列式.
设A=为n×n正定矩阵，证明：|A|≤a11 a22…ann.其中符号|∙|表示行列式.
设A是n阶正定矩阵，B为n阶实方阵，证明：(1)若B'=B,则AB的特征值为实数；(2)若B正定,则AB的特征值皆大于0；(3)若B正定,且AB=BA,则AB正定。