证 明 题（数学·2021年5月·阿里巴巴）

令n为正整数。对任一正整数k，记0_k=为k×k的零矩阵。令

Y=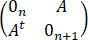

为一个(2n+1)×(2n+1)矩阵，其中A=(x_i,j)_{1≤i≤n,1≤j≤n+1}是一个n×(n+1)实矩阵且A^t记A的转置矩阵，即(n+1)×n的矩阵，(j,i)处元素为x_i,j.

(i)证明题（10分）称复数λ为k×k矩阵X的一个特征值，如果存在非零列向量

v=(x₁,…,x_k)^t

使得X_v=λv.证明：0是Y的特征值且Y的其他特征值形如±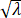，其中非负实数λ是AA^t的特征值。

(ii)证明题（15分）令n=3且a₁,a₂,a₃,a₄是4个互不相等的正实数。记

a=

以及

x_i,j=a_i δ_i,j+a_j δ_4,j-1/a² (a_i²+a₄²)a_j

(1≤i≤3,1≤j≤4)，其中δ_i,j=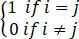 .证明：Y有7个互不相等的特征值。

解答提示

(i)记In=为n×n阶恒同矩阵.作初等变换可证det⁡(λI2n+1-Y)=λ det⁡(λ2 In-AAt ).所以，0是Y的特征值且Y的其他特征值形如±，其中λ是AAt的非负实数特征值.(ii)记u=(a1,a2,a3,a4 ),v=((a12+a42)/a,(a22+a42)/a,(a12+a42)/a).计算得AAt=diag{a12,…,a32 }+ut u-vt v.设f(s)=det⁡(sI...

查看完整答案，请下载word版