2021年全国统考考研试题-代数-矩阵-矩阵的运算

证明题（理工数学Ⅰ·2021年·全国统考）

已知A=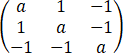

(1) 求正交矩阵P，使得P^TAP为对角矩阵；

(2) 求正定矩阵C，使得C² = (a+3)E-A.

解答提示

(1) 由|λE-A| = = (λ-a+1)2 (λ-a-a) = 0得λ1 = a+2,λ2 = λ3 = a-1当λ1 = a+2时((a+2)E-A) = 的特征向量α1 = 当λ2 = λ3 = a-1时((a+2)E-A) = 的特征向量α2 = ,α3 ...

查看完整答案，请下载word版

代数

当x→0时，用“o(x)”表示比x高阶的无穷小，则下列式子中错误的是【】

设an=a,且a≠0，则当n充分大时，有【】.

设{an}，{bn}，{cn}均为非负数列，且an=0， bn=1，cn=∞，则必有【】

2000年全国统考考研试题72

2003年全国统考考研试题73

设a≠，则ln= .

2004年全国统考考研试题75

设函数f(x)在（-∞,+∞）内单调有界，{xn}为数列，下列命题正确的是【】

设数列{xn}满足0<x1<π，xn+1=sinxn（n=1,2,...）.证明xn存在，并求该极限.

已知函数f(x)是周期为π的奇函数，且当x∈（0，π/2）时f(x)=sinx-cosx+2，则当x∈（π，π/2）时f(x)=.

矩阵

二次型f(x1,x2,x3 ) = (x1 + x2)2 + (x2 + x3)2 - (x3 - x1)2的正惯性指数依次为【】

设A,B为n阶实矩阵，下列结论不成立的是【】

设A = aij为3阶矩阵，Aij为代数余子式，若A的每行元素之和均为2，且|A| = 3，A11 + A21 + A31 = .

已知矩阵A=，若下三角可逆矩阵P和上三角可逆矩阵Q使PAQ为对角矩阵，则P,Q可以分别取【】

设矩阵A=仅有两个不同的特征值.若A相似于对角矩阵，求a,b的值，并求可逆矩阵P，使P-1AP为对角矩阵.

已知A=,B为三阶方阵，满足A2B=A+AB，求B。

方阵A=，而n≥2为整数，则A2-2An-1=。

A为4阶方阵，其特征值为-1,1,2,3，A*为A的伴随矩阵，则|A*|=。

已知A=,B=满足(E-A-1B) XT=A-1（其中E为单位阵），试求X。

设矩阵T=,T以及D可逆，证明(A-BD-1 C)-1存在，并求T-1，其中A,B,C,D为适当维度的矩阵。

矩阵的运算

已知A=(1) 求正交矩阵P，使得PTAP为对角矩阵；(2) 求正定矩阵C，使得C2 = (a+3)E-A.

令n为正整数。对任一正整数k，记0k=为k×k的零矩阵。令Y=为一个(2n+1)×(2n+1)矩阵，其中A=(xi,j)1≤i≤n,1≤j≤n+1是一个n×(n+1)实矩阵且At记A的转置矩阵，即(n+1)×n的矩阵，(j,i)处元素为xi,j.(i)证明题（10分）称复数λ为k×k矩阵X的一个特征值，如果存在非零列向量v=(x1,…,xk)t使得Xv=λv.证明：0是Y的特征值且Y的其他特征值形如±，其中非负实数λ是AAt的特征值。(ii)证明题（15分）令n=3且a1,a2,a3,a4是4个互不相等的正实数。记a=以及xi,j=ai δi,j+aj δ4,j-1/a2 (ai2+a42)aj(1≤i≤3,1≤j≤4)，其中δi,j= .证明：Y有7个互不相等的特征值。

若x=(-1,2,3,0,4)，求‖x‖1,‖x‖2,‖x‖∞.

设A=，求‖x‖1,‖x‖F,‖x‖∞.

设A是n阶矩阵，A*为A的伴随矩阵，证明秩R(A*)与R(A)之间满足R(A* )=

设A=(aij)是n阶实对称正定矩阵，b1,b2,…,bn为任意非零实数，证明B=(aijbibj)也是正定的。

设A为任一n阶矩阵，数λ>0，证明λI+AT A为正定矩阵。

设A≠0，证明：R(A)=1的充要条件是A可表示为一个列向量与一个行向量的乘积。

若n维列向量α与β正交，A=αβT，则A的特征值全为零。

A=，则A的特征值为【】