如图，在△ABC中，AB=AC，AD⊥BC于点D，BC=10cm，AD=8cm.点P从点B出发，在线段BC上以每秒3cm的速度向点C匀速运动，与此同时，垂直于AD的直线m从底边BC出发，以每秒2cm的速度沿DA方向匀速平移，分别交AB、AC、AD于点E、F、H. 当点P到达点C时，点P与直线m同时停止运动。设运动时间为t秒(t>0)。

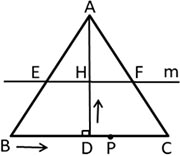
(1)当t=2时，连接DE、DF，求证四边形AEDF是菱形；

(2)在整个运动过程中，所形成的△PEF的面积存在最大值。当△PEF的面积最大时，求线段BP的长；

(3)是否存在某一时刻t，使△PEF是直角三角形？若存在，请求出此刻t的值；若不存在，请说明理由。