2022年重庆市初中学业水平考试(中考)数学试卷(B卷)

③以 、 为对角线时， ，解得

【点睛】本题考查了二次函数的解析式、一次函数的解析式、二次函数的性质、平行四边形的性质、相似三角形的判定和性质等知识点，解题的关键是能够熟练应用待定系数法求得二次函数和一次函数解析式．

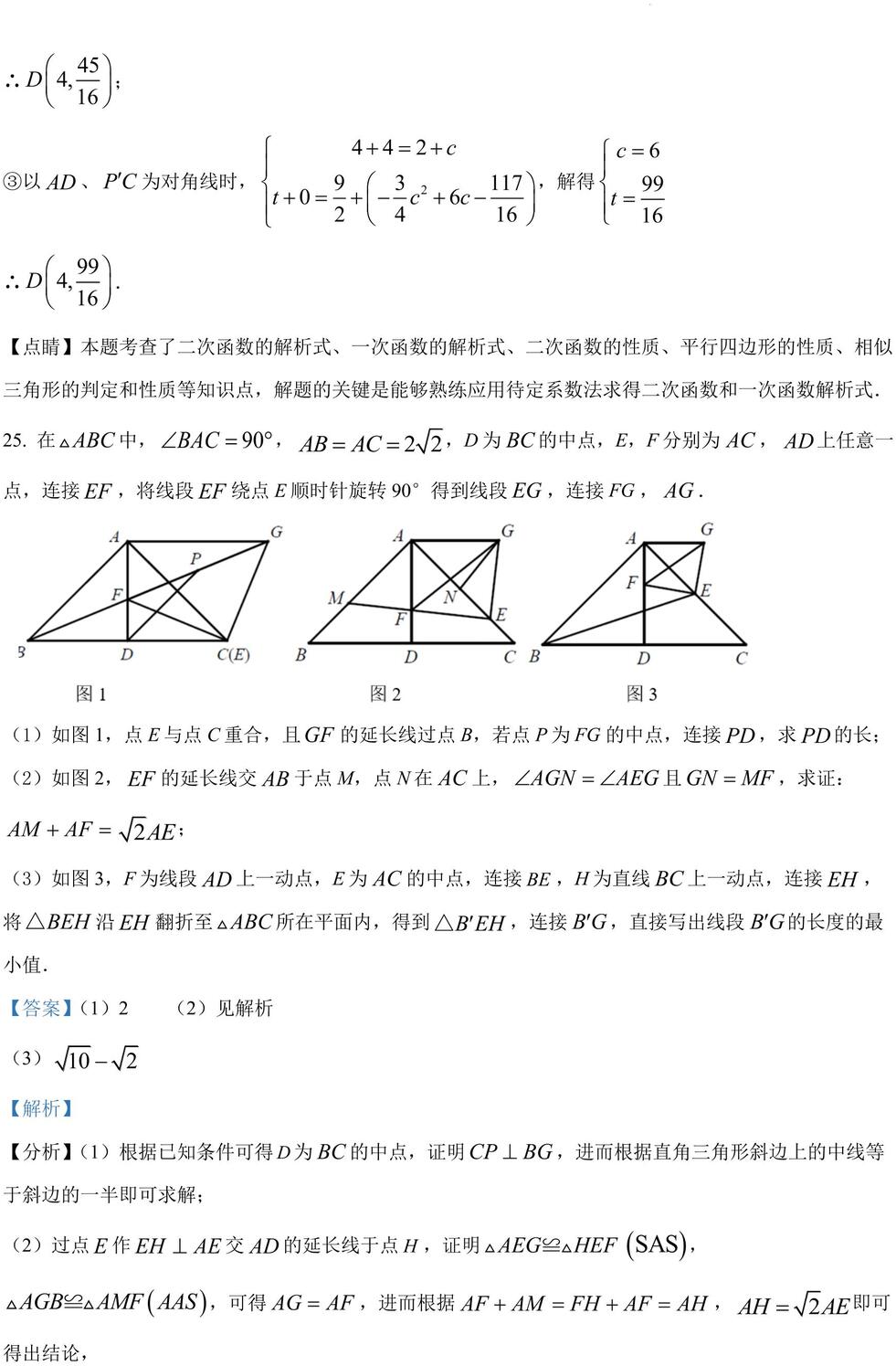
25. 在 中， ， ，D 为 的中点，E，F 分别为 ， 上任意一点，连接 ，将线段 绕点 E顺时针旋转 90°得到线段 ，连接 ， ．

（1）如图 1，点 E 与点 C重合，且 的延长线过点 B，若点 P 为 的中点，连接 ，求 的长；

（2）如图 2， 的延长线交 于点 M，点 N 在 上， 且 ，求证：

（3）如图 3，F 为线段 上一动点，E 为 的中点，连接 ，H 为直线 上一动点，连接 ，将 沿 翻折至 所在平面内，得到 ，连接 ，直接写出线段 的长度的最小值．

【答案】（1）2 （2）见解析

【分析】（1）根据已知条件可得 为 的中点，证明 ，进而根据直角三角形斜边上的中线等于斜边的一半即可求解；

（2）过点 作 交 的延长线于点 ，证明 ，

，可得 ，进而根据 ， 即可得出结论，