-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
∴2a+c＝0，故③符合题意．
④由图象可知：二次函数 y＝ax2+bx+c 的最小值小于 0， 令 y＝1代入 y＝ax2+bx+c，
∴ax2+bx+c＝1 有两个不相同的解，故④不符合题意． 故选：D．
【点睛】本题考查二次函数的图像与系数的关系，解题的关键是正确地由图象得出 a、b、
c 的数量关系，本题属于基础题型．
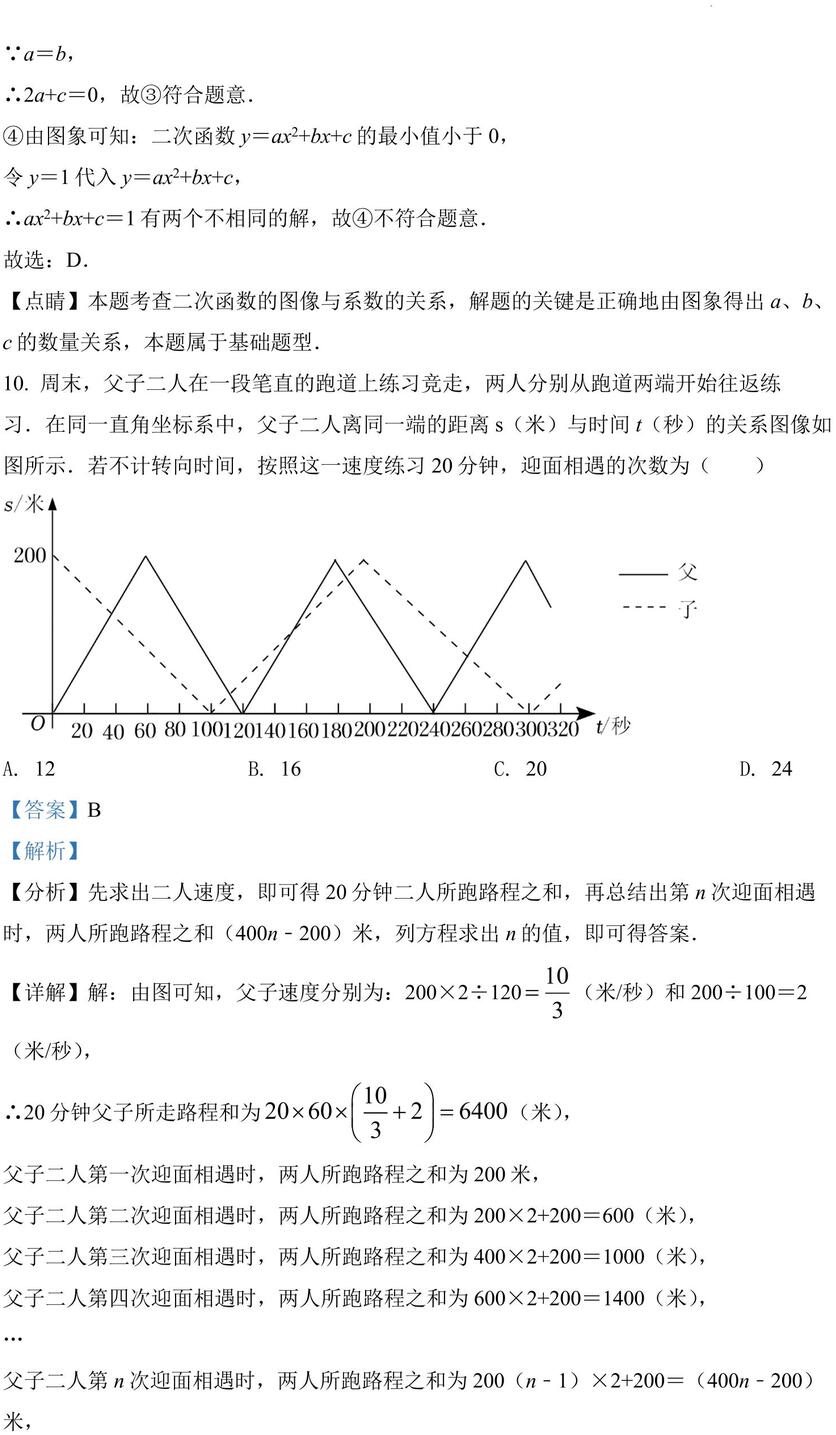
10. 周末，父子二人在一段笔直的跑道上练习竞走，两人分别从跑道两端开始往返练习．在同一直角坐标系中，父子二人离同一端的距离 s（米）与时间 t（秒）的关系图像如图所示．若不计转向时间，按照这一速度练习 20 分钟，迎面相遇的次数为（ ）
【分析】先求出二人速度，即可得 20 分钟二人所跑路程之和，再总结出第 n 次迎面相遇时，两人所跑路程之和（400n﹣200）米，列方程求出 n 的值，即可得答案．
【详解】解：由图可知，父子速度分别为：200×2÷120 （米/秒）和 200÷100＝2
（米/秒），
∴20 分钟父子所走路程和为 （米）， 父子二人第一次迎面相遇时，两人所跑路程之和为 200 米， 父子二人第二次迎面相遇时，两人所跑路程之和为 200×2+200＝600（米）， 父子二人第三次迎面相遇时，两人所跑路程之和为 400×2+200＝1000（米）， 父子二人第四次迎面相遇时，两人所跑路程之和为 600×2+200＝1400（米）， 父子二人第 n 次迎面相遇时，两人所跑路程之和为 200（n﹣1）×2+200＝（400n﹣200）米，