2022年江西省初中学业水平考试(中考)数学试卷

【小问 3详解】

“双减”前共调查 500 个数据，从小到大排列后，第 250 个和第 251 个数据均为 1，

∴“双减”前学生报班个数的中位数为 1，

“双减”后学生报班个数出现次数最多的是 0，

∴“双减”后学生报班个数的众数为 0， 故答案为：1；0；

②从“双减”前后学生报班个数的变化情况说明：“双减”政策宣传落实到位，参加校外培训机构的学生大幅度减少，“双减”取得了显著效果．

【点睛】本题考查统计的应用，理解题意，对数据进行采集和整理，掌握中位数和众数的概念是解题关键．

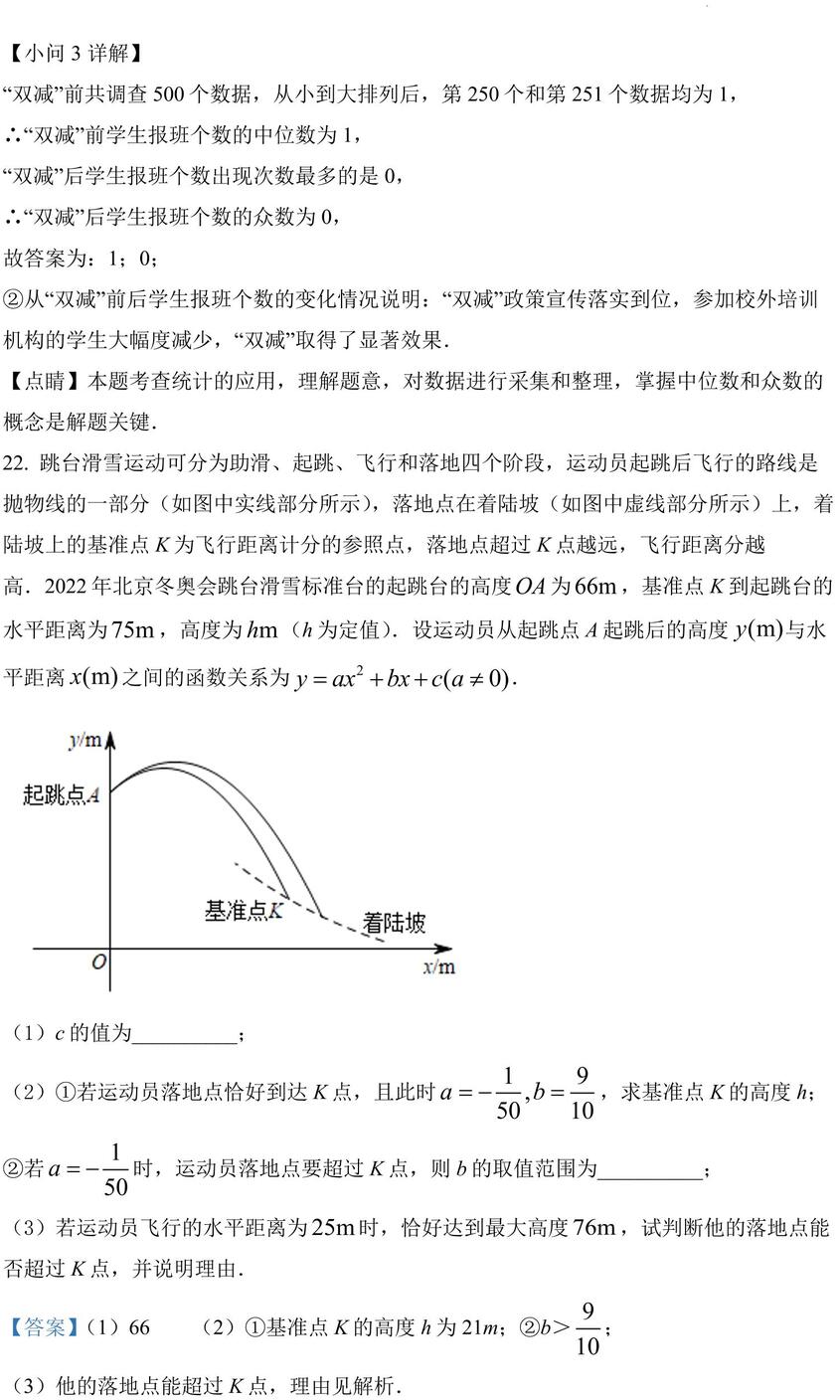
22. 跳台滑雪运动可分为助滑、起跳、飞行和落地四个阶段，运动员起跳后飞行的路线是抛物线的一部分（如图中实线部分所示），落地点在着陆坡（如图中虚线部分所示）上，着陆坡上的基准点 K 为飞行距离计分的参照点，落地点超过 K 点越远，飞行距离分越高．2022年北京冬奥会跳台滑雪标准台的起跳台的高度 为 ，基准点 K到起跳台的水平距离为 ，高度为 （h 为定值）．设运动员从起跳点 A起跳后的高度 与水平距离 之间的函数关系为 ．

（1）c 的值为__________；

（2）①若运动员落地点恰好到达 K 点，且此时 ，求基准点 K 的高度 h；

②若 时，运动员落地点要超过 K 点，则 b 的取值范围为__________；

（3）若运动员飞行的水平距离为 时，恰好达到最大高度 ，试判断他的落地点能否超过 K 点，并说明理由．

【答案】（1）66 （2）①基准点 K 的高度 h 为 21m；②b＞ ；

（3）他的落地点能超过 K 点，理由见解析．