2022年江苏省扬州市初中学业水平考试(中考)数学试卷

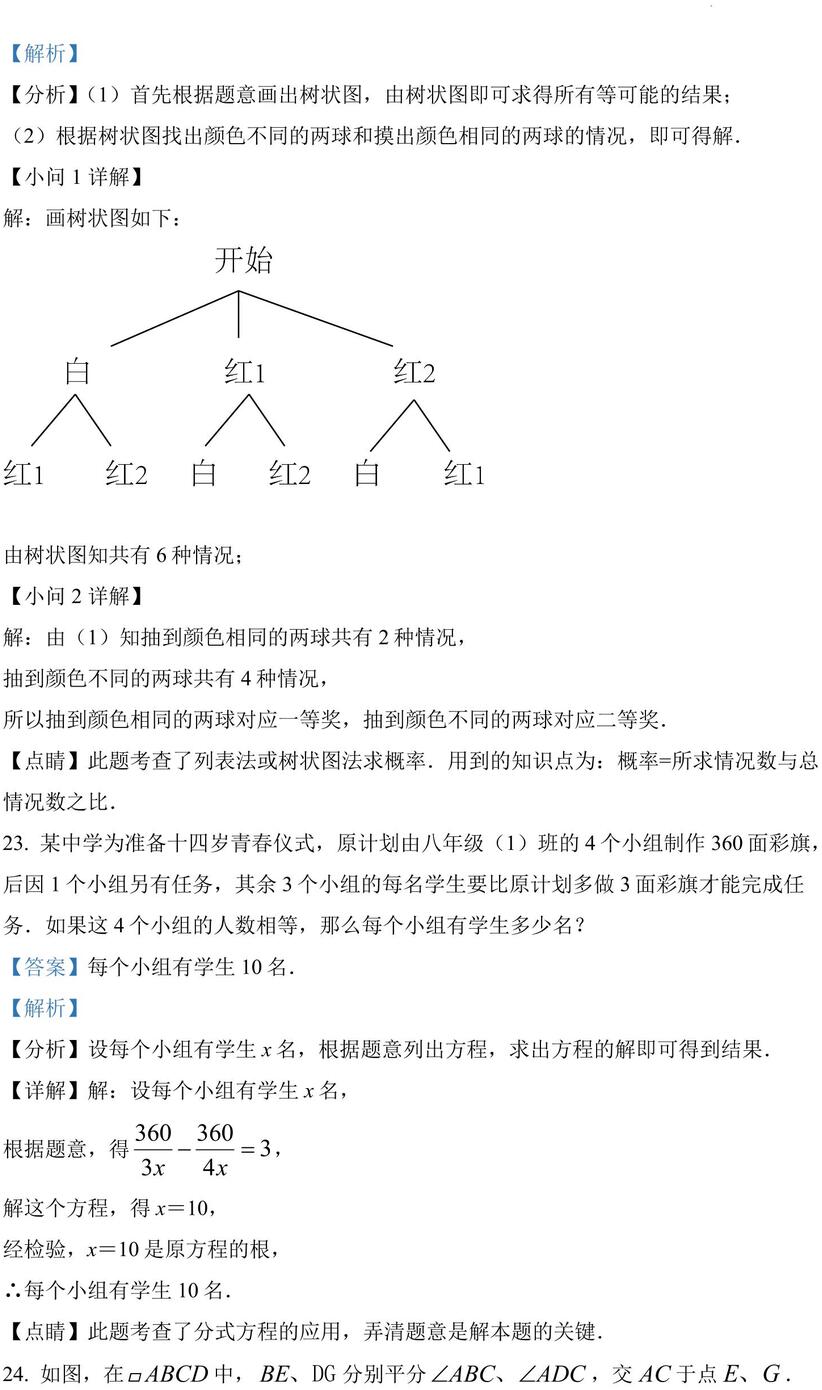
【分析】（1）首先根据题意画出树状图，由树状图即可求得所有等可能的结果；

（2）根据树状图找出颜色不同的两球和摸出颜色相同的两球的情况，即可得解．

【小问 1详解】 解：画树状图如下： 由树状图知共有 6种情况；

【小问 2详解】 解：由（1）知抽到颜色相同的两球共有 2种情况， 抽到颜色不同的两球共有 4种情况， 所以抽到颜色相同的两球对应一等奖，抽到颜色不同的两球对应二等奖．

【点睛】此题考查了列表法或树状图法求概率．用到的知识点为：概率=所求情况数与总情况数之比．

23. 某中学为准备十四岁青春仪式，原计划由八年级（1）班的 4 个小组制作 360 面彩旗，后因 1 个小组另有任务，其余 3 个小组的每名学生要比原计划多做 3 面彩旗才能完成任务．如果这 4 个小组的人数相等，那么每个小组有学生多少名？

【答案】每个小组有学生 10 名．

【分析】设每个小组有学生 x 名，根据题意列出方程，求出方程的解即可得到结果．

【详解】解：设每个小组有学生 x 名， 根据题意，得 ， 解这个方程，得 x＝10， 经检验，x＝10 是原方程的根，

∴每个小组有学生 10 名．

【点睛】此题考查了分式方程的应用，弄清题意是解本题的关键．

24. 如图，在 中， 分别平分 ，交 于点 ．