对于n个元素的关键码序列{k1,k2,…,kn},当且仅当满足下列关系时称其为堆。
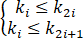 或
或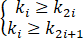
以下关键码序列中,【 】不是堆。
A、12,25,22,53,65,60,30
B、12,25,22,30,65,60,53
C、65,60,25,22,12,53,30
D、65,60,25,30,53,12,22
对于n个元素的关键码序列{k1,k2,…,kn},当且仅当满足下列关系时称其为堆。
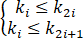 或
或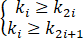
以下关键码序列中,【 】不是堆。
A、12,25,22,53,65,60,30
B、12,25,22,30,65,60,53
C、65,60,25,22,12,53,30
D、65,60,25,30,53,12,22
C
对n个记录进行非递减排序,在第一趟排序之后,一定能把关键码序列中的最大或最小元素放在其最终排序位置上的排序算法是【 】。
设有二叉排序树如下图所示,根据关键码序列【 】可构造出该二叉排序树。
某图G的邻接矩阵如下所示。以下关于该图的叙述中,错误的是【 】
某二又树的先序遍历序列为 ABCDFGE,中序遍历序列为 BAFDGCE。以下关于该二又树的叙述中,正确的是【 】。
队列采用如下图所示的循环单链表表示,左图表示队列为空,右图为e1、e2、e3依次入队列后的状态,其中,rear指针指向队尾元素所在结点,size为队列长度。以下叙述中,正确的是【 】。
设有初始为空的栈S,对于入栈序列a、b、c、d,经由一个合法的进栈和出栈操作序列后(每个元素进栈、出栈各1次),以c作为第一个出栈的元素时,不能得到的序列为【 】。
对于长度为n的线性表(即n个元素构成的序列),若采用顺序存储结构(数组存储),则在等概率下,删除一个元素平均需要移动的元素数为【 】。
对长度为10的线性表进行冒泡排序,最坏情况下需要比较的次数为__________。
初始序列为1 8 6 2 5 4 7 3一组数采用堆排序,当建堆(小根堆)完毕时,堆所对应的二叉树中序遍历序列为【 】。
回答问题并写出推导过程:对50个整数进行快速排序需进行关键字间比较次数可能达到的最大值和最小值各为多少?
在起泡(冒泡)排序过程中,有的关键字在某趟排序中可能朝着与最终排序相反的方向移动,请举例说明之。快速排序过程中有没有这种现象?
快速排序的最大递归深度是__________,最小递归深度是__________。
快速排序的速度在所有排序方法中为最快,而且所需附加的空间也最少。
若需在O(log2n)的时间内完成对数组的排序,且要求排序是稳定的,则可选择的排序方法是【 】。
在文件“局部有序”或文件长度较小的情况下,最佳内部排序的方法是【 】。
下述排序算法中,所需辅助存储量最多的是__________,所需辅助存储量最少的是__________,平均速度最快的是__________。A. 快速排序 B. 归并排序 C. 堆排序