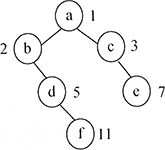
对二叉树中的结点如下编号：树根结点编号为1，根的左孩子结点编号为2、右孩子结点编号为3，以此类推，对于编号为i的结点，其左孩子编号为2i、右孩子编号为2i+1。例如，下图所示二又树中有6个结点，结点a、b、c、d、e、f的编号分别为1、2、3、5、7、11。那么，当结点数为n(n>0)的【 】时，其最后一个结点编号为2n-1。
A、二叉树为满二叉树(即每层的结点数达到最大值)
B、二叉树中每个内部结点都有两个孩子
C、二叉树中每个内部结点都只有左孩子
D、二又树中每个内部结点都只有右孩子
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
单项选择（2016年春程序员软考）
答案解析
D当二叉树为满二叉树时，第i层上最后一个结点的编号为2i-1，第2层最后一个结点的编号为22-1，第3层最后一个节点的编号为23-1。要使得结点数n与高度一致，应使得每层只有一个结点，并且每层的结点都...
查看完整答案讨论
队列采用如下图所示的循环单链表表示，左图表示队列为空，右图为e1、e2、e3依次入队列后的状态，其中，rear指针指向队尾元素所在结点，size为队列长度。以下叙述中，正确的是【 】。
设有初始为空的栈S，对于入栈序列a、b、c、d，经由一个合法的进栈和出栈操作序列后(每个元素进栈、出栈各1次)，以c作为第一个出栈的元素时，不能得到的序列为【 】。
对于长度为n的线性表(即n个元素构成的序列)，若采用顺序存储结构(数组存储)，则在等概率下，删除一个元素平均需要移动的元素数为【 】。
某有向图G及其邻接矩阵如下所示。以下关于图的邻接矩阵存储的叙述中，错误的是【 】。
最优二叉树(或哈夫曼树)是指权值为w1，w2，…，wn的n个叶结点的二叉树中带权路径长度最小的二叉树。【 】是哈夫曼树(叶结点中的数字为其权值)。