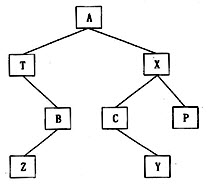
对下列二叉树进行后序遍历的结果是【 】
A、ZBTYCPXA
B、ATBZXCYP
C、ZBTACYXP
D、ATBZXCPY
对下列二叉树进行后序遍历的结果是【 】

A、ZBTYCPXA
B、ATBZXCYP
C、ZBTACYXP
D、ATBZXCPY
A
【解析】
按照二叉树后序遍历的方法:
在访问根结点、遍历左子树与遍历右子树这三者中,首先遍历左子树,然后遍历右子树,最后访问根结点;并且,在遍历左、右子树时,仍然先遍历左子树,然后遍历右子树,最后访问根结点。
对本题中的二叉树进行后序遍历的结果应是ZBTYCPXA。
对二叉排序树进行【 】遍历,可以得到该二叉树所有结点构成的排序序列。
若二叉树采用二叉链表存储结构,要交换其所有分支结点左右子树的位置,利用【 】遍历方法最合适。
已知一棵二叉树,如果先序遍历的顺序是ADCEFGHB,中序遍历的顺序是CDFEGHAB,则后序遍历的结果为【 】。
具有n个叶子的二叉树,每个叶子的权值为wi(1≤i≤n),其中带权路径长度最小的二叉树称为__________。
啥夫曼树是带权路径长度最短的树,路径上权值较大的结点离根较近。
在有 6 个字符组成的字符集 S 中,各个字符出现的频次分别为 3、4、5、6、8、10,为 S 构造的哈夫曼树的加权平均长度为【 】