已知序列17，31，13，11，20，35，25，8，4，11，24，40，27，请画出该序列的二叉排序树，并分别给出下列操作后的二叉排序树：
① 插入数据9；
② 删除结点17；
③ 再删除结点13。
-
关注优题吧，注册平台账号.
题吧，智能辅助学习中心
问答题（1996年中国科学技术大学）
答案解析
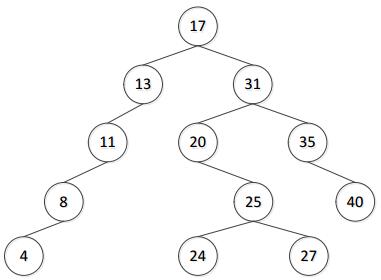
该序列的二叉排序树：
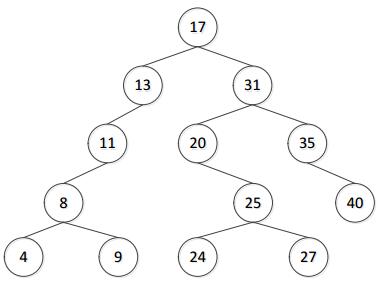
插入数据9后的二叉排序树：
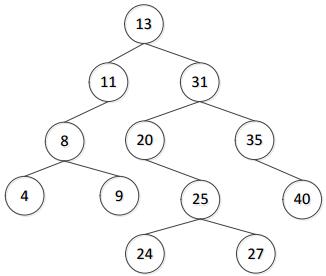
删除17后的二叉排序树：
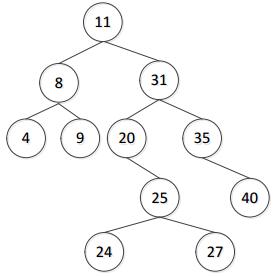
删除13后的二叉排序树：
讨论
用向量和单链表表示的有序表均可使用折半查找方法来提高查找速度。
在分块检索中，对256个元素的线性表分成__________块最好，每块的最佳长度是__________；若每块的长度为8，其平均检索长度为__________。
有n个数存放在一维数组A[1..n]中，在进行顺序查找时，这n个数的排列有序或无序其平均查找长度不同。
在n个记录的有序顺序表中进行折半查找，最大的比较次数是__________。
用二分法查找一个线性表时，该线性表必须具有的特点是____________。
对含有 600 个元素的有序顺序表进行折半查找，关键字之间的比较次数最多是【 】
在分块检索中，若索引表和各块内均用顺序查找，则有900个元素的线性表分成__________块最好；若分成25块，其平均查找长度为__________。
下列关于非空 B 树的叙述中，正确的是【 】Ⅰ. 插入操作可能增加树的高度Ⅱ. 删除操作一定会导致叶结点的变化Ⅲ. 查找某关键字一定是要查找到叶结点Ⅳ. 插入的新关键字最终位于叶结点中
利用逐点插入法建立序列（50，72，43，85，75，20，35，45，65，30）对应的二叉排序树以后，查找元素35要进行【 】次元素间的比较。
在关键字随机分布的情况下，用二叉排序树的方法进行查找，其查找长度与【 】量级相当。
在任意一棵非空二叉排序树中，删除某结点后又将其插入，则所得二叉排序树与删除前原二叉排序树相同。
设有关键码序列(10，40，30，20)，根据该序列构建的二叉排序树是【 】。
设有二叉排序树如下图所示，根据关键码序列【 】可构造出该二叉排序树。
一棵满二叉排序树深度为k，节点数为2k-1；节点值为1至（2k - 1），给出k和任意三个节点的值，输出包含该三个节点的最小子树的根节点。样例输入：4 10 15 13样例输出：12
在分析二叉查找树性能时常加入失败结点，即外结点，从而形成扩充的二叉树。若设失败结点i所在层次为li，那么查找失败到达失败结点时所做的数据比较次数是多少？
某二叉排序树如下所示，新的元素45应作为【 】插入该二叉树中。
在一个有n个顶点的无向网中，有O(n1.5*log2n)条边，则应该选用【 】算法来求这个网的最小生成树，从而使计算时间较少。
G是一个非连通无向图，共有28条边，则该图至少有【 】个顶点。
如果只考虑有序树的情形，那么具有7个结点的不同形态的树共有【】
在叶子数目和权值相同的所有二叉树中，最优二叉树一定是完全二叉树，该说法【 】。
n个顶点的连通图用邻接矩阵表示时，该矩阵至少有__________个非零元素。
栈的输入序列为1,2,3,...,n，输出序列为a1,a2,a3,...,an，若ai=n(1≤i≤n)，则有 ak>ak+1>an。