证 明 题（理工数学Ⅰ·1994年·全国统考）
设四元线性齐次方程组(Ⅰ)为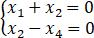
，又知某线性齐次方程组(Ⅱ)的通解为k1 (0,1,1,0)+k2 (-1,2,2,1).
(1)求线性方程组(Ⅰ)的基础解系；
(2)问线性方程组(Ⅰ)和(Ⅱ)是否有非零公共解？若有，则求出所有的非零公共解.若没有，则说明理由.
解答提示
(1)由题设，(Ⅰ)的系数矩阵为，易求得其基础解系为(0,0,1,0),(-1,1,0,1)，其通解为k3(0,0,1,0)+k4(-1,1,0,1).(2)令k1 (0,1,1,0)+k2 (-1,2,2,...
查看完整答案，请下载word版
设x1-x2=a1,x2-x3=a2,x3-x4=a3,x4-x5=a4,x5-x1=a5。证明此方程组有解的充分必要条件为ai =0。
设A为m×n矩阵，非齐次线性方程组Ax ̅=β ̅有唯一解的充分必要条件为：.
当λ,μ为何值时，方程组有惟一解？无解？有无穷解？无穷解时并求其全解.
设A为n阶方阵，A*为A的伴随矩阵且A11≠0,b≠0，其中A11为A的a11对应的代数余子式.证明：AX=b有无穷多个解⟺b是A* X=0的解.
问a,b为何值时，线性方程组有唯一解？无解？有无穷解？并求出有无穷解时的通解.
已知β1,β2是非齐次线性方程组Ax=b的两个不同的解，α1,α2是对应齐次线性方程组Ax=0的基础解系，k1,k2为任意常数，则方程组Ax=b的通解（一般解）必是【 】
不查表，求方程x2sin=2x-1977的近似解，精确到0.001.
设3阶矩阵A=(α1,α2,α3)，B=(β1,β2,β3)，若向量组α1,α2,α3可以由向量组β1,β2线性表出，则【 】
设A=(α1,α2,α3,α4)为4阶正交矩阵，若矩阵A = ,β = ,k表示任意常数，则线性方程组Ax=β的通解为x=【 】
设线性方程组Ax=b的系数矩阵A=。(1)试求能使Jacobi迭代法收敛的a的取值范围；(2)对该方程组写出Jacobi迭代格式（设b=(b1,b2,b3)T已知）。
对方程组，试问用Jacobi迭代和Gauss-Seidel迭代是否收敛？为什么？