证 明 题（数学·1995年·全国统考）
某地为促进淡水鱼养殖业的发展,将价格控制在适当范围内,决定对淡水鱼养殖提供政府补贴.设淡水鱼的市场价格为x元/千克,政府补贴为t元/千克.根据市场调查,当8≤x≤14时,淡水鱼的市场日供应量P千克与市场日需求量Q千克近似地满足关系:
P=1000(x+t-8)(x≥9,t≥0),
Q=500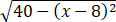
(8≤x≤14).
当P=Q时的市场价格称为市场平衡价格.
(1)将市场平衡价格表示为政府补贴的函数,并求出函数的定义域;
(2)为使市场平衡价格不高于每千克10元,政府补贴至少为每千克多少元?
解答提示
(1)依题设有1000(x+t-8)=500,化简得x2+(8t-80)x+(4t2-64t+280)=0.当判别式∆=800-16t2≥0时，可得x=8-4/5 t±2/5 .由∆≥0,t≥0,8≤x≤14，得不等式组：① ② 解不等式组①，得0...
查看完整答案，请下载word版
函数 f(x) = x4 − 2x3 的图像在点 (1, f(1)) 处的切线方程为【 】。
若 x, y 满足约束条件 则 z = x + 7y 的最大值为 .
设 {an} 是公比不为 1 的等比数列, a1 为 a2, a3 的等差中项.(1) 求 {an} 的公比;(2) 若 a1 = 1, 求数列 {nan} 的前 n 项和.
已知函数 f(x) = |3x + 1| − 2|x − 1|.(1) 画出 y = f(x) 的图像;(2) 求不等式 f(x) > f(x + 1) 的解集.
正实数x,y,z,w满足x≥y≥w，且x+y≤2(w+z)，求 + 的最小值.
若f(x)=x5+px+q有有理根，且正整数p,q不大于100，则满足条件的(p,q)共有几组.
已知x,y,z>0，判断s=x/(x+y) + y/(y+z) + z/(z+x) 是否存在最大值与最小值.
已知数列{an}满足：a1=1，a2=4,且an2 - an-1an+1=2n-1(n≥2,n∈N*)，求a2020的个位数.
已知函数 f(x) = ex + ax2 − x.(1) 当 a = 1 时, 讨论 f(x) 的单调性;(2) 当 x ⩾ 0 时, f(x) ⩾ x3 + 1, 求 a 的取值范围.
设函数 f(x) = ln|2x + 1| − ln|2x − 1|, 则 f(x)【 】
设函数 f(x) = x3 − 1/x3 , 则 f(x)【 】
已知函数 f(x) = x3 − kx + k2.(1) 讨论 f(x) 的单调性;(2) 若 f(x) 有三个零点, 求 k 的取值范围.
若定义在 R 的奇函数 f(x) 在 (−∞, 0) 单调递减, 且 f(2) = 0, 则满足 xf(x − 1) ⩾ 0 的 x 的取值范围是【 】