-
关注“蜜蜂引路”，分配平台账号.
题吧，智能辅助学习中心
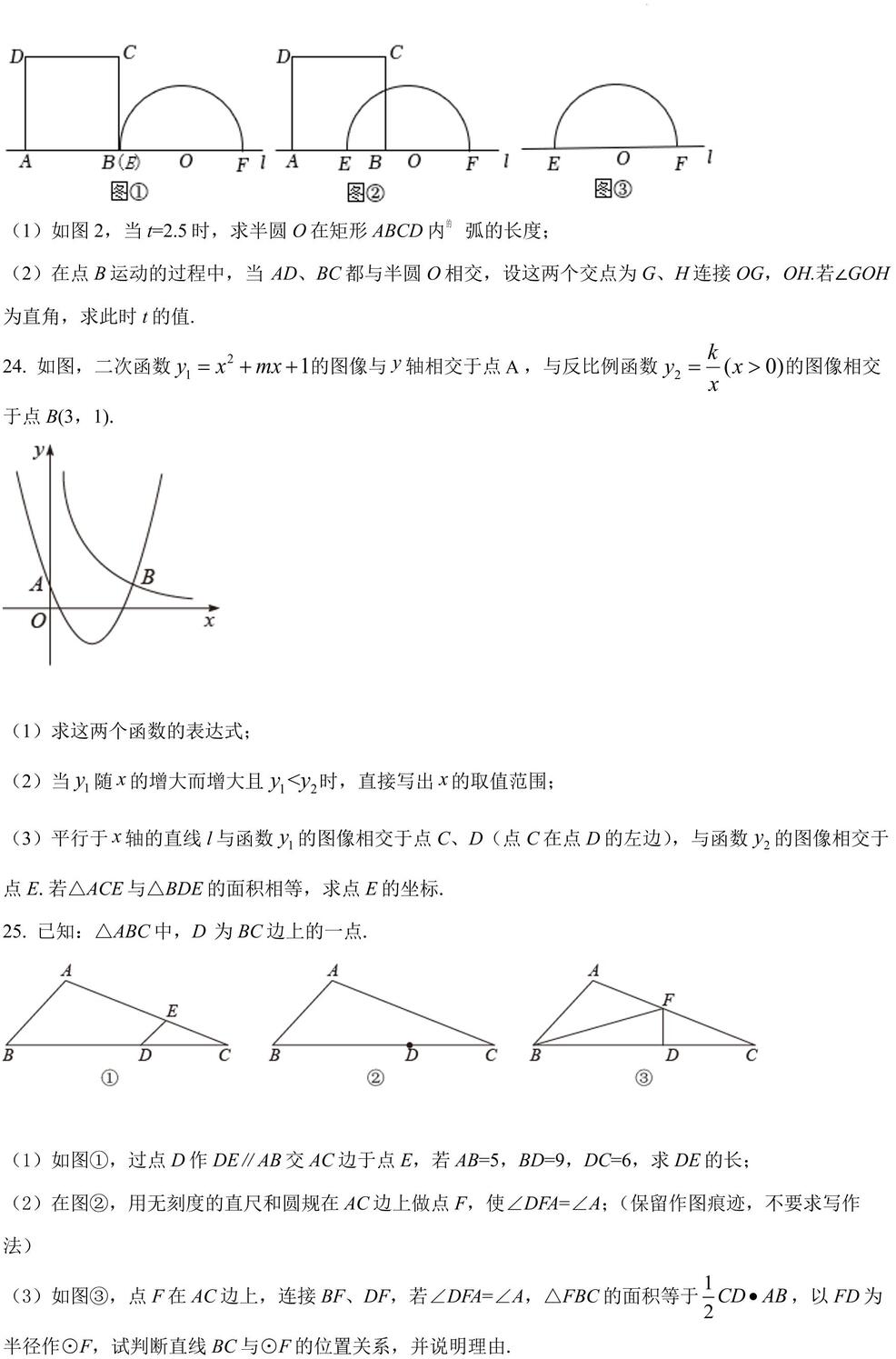
（1）如图 2，当 t=2.5 时，求半圆 O 在矩形 ABCD 内 弧的长度；
（2）在点 B 运动的过程中，当 AD、BC都与半圆 O 相交，设这两个交点为 G、H连接 OG，OH.若∠GOH为直角，求此时 t 的值.
24. 如图，二次函数 的图像与 轴相交于点 ，与反比例函数 的图像相交于点 B(3，1).
（1）求这两个函数的表达式；
（2）当 随 的增大而增大且 时，直接写出 的取值范围；
（3）平行于 轴的直线 l 与函数 的图像相交于点 C、D（点 C 在点 D 的左边），与函数 的图像相交于点 E.若△ACE 与△BDE 的面积相等，求点 E 的坐标.
25. 已知：△ABC 中，D 为 BC 边上的一点.
（1）如图①，过点 D 作 DE∥AB 交 AC 边于点 E，若 AB=5，BD=9，DC=6，求 DE 的长；
（2）在图②，用无刻度的直尺和圆规在 AC 边上做点 F，使∠DFA=∠A；（保留作图痕迹，不要求写作法）
（3）如图③，点 F 在 AC 边上，连接 BF、DF，若∠DFA=∠A，△FBC 的面积等于 ，以 FD 为半径作⊙F，试判断直线 BC 与⊙F 的位置关系，并说明理由.