-
关注“优题吧”，分配平台账号.
题吧，智能辅助学习中心
考研2024年西安交通大学( )
求不定积分∫sin(lnx)dx=________.
考研2023年理工数学Ⅱ( )
函数f(x)=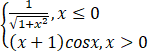
的一个原函数为【 】
A、F(x)=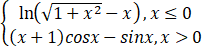
B、F(x)=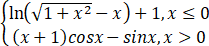
C、F(x)=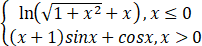
D、F(x)=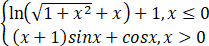
F(x)=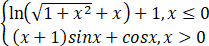
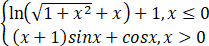
竞赛1995年南京大学( )
求∫(1+x)/(x(1+xex)) dx.
因为(xex )'=ex (x+1)，令xex=t，则
∫(1+x)/(x(1+xex)) dx=∫(ex (1+x))/(xex (1+xex)) dx=∫1/(t(1+t)) dt
=∫(1/t-1/(1+t))dt=ln|t/(1+t)|+C=ln|(xex)/(1+xex )|+C
考研1990年理工数学Ⅱ( )
计算∫lnx/(1-x)2 dx.
原式=∫lnx d(1/(1-x))=lnx/(1-x)-∫1/(x(1-x)) dx
=lnx/(1-x)-∫(1/x+1/(1-x)) dx=lnx/(1-x)+ln|(1-x)/x|+C.
考研1990年理工数学Ⅱ( )
设函数f(x)在(-∞,+∞)上连续，则d∫f(x) dx等于【 】
A、f(x)
B、f(x)dx
C、f(x)+C
D、f’(x)
f(x)dx