2021年全国统考考研试题-概率统计-假设检验

单项选择（理工数学Ⅰ·2021年·全国统考）

设X₁,X₂,…,X₁6为来自总体N(μ,4)的简单随机样本.考虑假设检验问题：H₀:μ≤10,H₁:μ>10.Φ(x)表示标准正态分布函数，若该检验问题的拒绝域为W={X ̅≥11}，其中X ̅=1/16·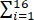X_i ，则μ=11.5时，该检验犯第二类错误的概率为【】

A、1 - Φ(0.5)

B、1 - Φ(1)

C、1 - Φ(1.5)

D、1 - Φ(2)

解答提示

B

考研

当x→0时，用“o(x)”表示比x高阶的无穷小，则下列式子中错误的是【】

设an=a,且a≠0，则当n充分大时，有【】.

设{an}，{bn}，{cn}均为非负数列，且an=0， bn=1，cn=∞，则必有【】

2000年全国统考考研试题72

2003年全国统考考研试题73

设a≠，则ln= .

2004年全国统考考研试题75

设函数f(x)在（-∞,+∞）内单调有界，{xn}为数列，下列命题正确的是【】

设数列{xn}满足0<x1<π，xn+1=sinxn（n=1,2,...）.证明xn存在，并求该极限.

已知函数f(x)是周期为π的奇函数，且当x∈（0，π/2）时f(x)=sinx-cosx+2，则当x∈（π，π/2）时f(x)=.

概率统计

设A,B为随机事件，且0<P(B)<1，下列命题中为假命题的是【】

设(X1,Y1 ),(X2,Y2 ),…,(Xn,Yn )为来自总体N(μ1,μ2;σ12,σ22;ρ)的简单随机样本. 令θ=μ1 - μ2, X ̅=1/n·Xi ,Y ̅=1/n·Yi ,θ ̂=X ̅ - Y ̅，则【】

甲乙两个盒子中各装有2个红球和2个白球，先从甲盒中任取一球，观察颜色后放入乙盒中，再从乙盒中任取一球.令X，Y分别表示从甲盒和乙盒中取到的红球个数，则X与Y的相关系数.

在区间(0,2)上随机取一点，将该区间分成两段，较短的一段长度记为X，较长的一段记为Y，令Z=Y/X.(1) 求X的概率密度；(2) 求Z的概率密度；(3) 求E(X/Y).

总体X的概率分布为P{X=1}=(1-θ)/2,P{X=1}=P{X=3}=(1+θ)/4，利用来自总体X的样本观察值1,3,2,2,1,3,1,2可得θ的最大似然估计值为【】

蚂蚁森林是全球最大的个人碳账户平台，该平台以量化方式记录每个人的低碳行为。当支付宝用户收集到足够的“能量”时，他/她可以向蚂蚁森林申请种植一棵真正的树。截至2019年4月22日(世界地球曰)，支付宝蚂蚁森林的5亿用户已经在中国西北地区种植了1亿棵真树，总面积为11.2万公顷，保护着总面积为1.2万公顷的保护地。1.本题两小问中考虑在一个3×4的长方形区域的每个小方格的中心点种树，要求在横、竖、斜3个方向上都不能存在连续的3颗(及以上)树。令1表示可以种树，0表示不可以种树。满足种树条件的示意图为不满足种树条件的示意图为(a)请问在一个3×4的区域里，最多能种多少颗树，并给出一种种植的方式。(b) 在满足上一问最多能种多少颗树答案的前提下，请问一共有多少种种法，给出思路和答案。2. 考虑一个由从左到右的n个小方格组成的1×n的区域，从左向右依次在每个小方格种一棵树，一共种n棵。树的种类只有两种：胡杨和樟子松。假设在第一个小方格种植的树是胡杨的概率是r。后续种树的规则为：如果前一个小方格种的是胡杨，则本格种胡杨的概率为s；如果前一个小方格种的是樟子松，则本格种樟子松的概率为t,0<r,s,t<1。(a)假设r=1/3,s+t≠1。是否存在s和t，使得对任意的i,2≤i≤n，在第i个小方格种植的树是胡杨的概率都等于一个跟i无关的常数？如果存在，请给出s和t的关系；如果不存在，请说明理由。(b) 假设r=1/3,s=3/4,t=4/5。假设我们观察到第2019个小方格里种植的树是胡杨，但我们观察不到在其它小方格里种植的是哪种树。请问在第一个小方格里种植的树是胡杨的概率是多少？3.为了种树的可持续发展控制成本，蚂蚁森林希望在知道用户申请数量之前从公益机构获得种植配额。令随机变量D1和D2分别表示支付宝用户对胡杨和樟子松的申请数量。将Di的分布函数记为Fi，其均值和方差分别表示为μi和σi2(i=1,2)。假设蚂蚁森林只知道μi和σi2 (i=1,2)但并不知道F的其它信息。蚂蚁森林需要确定两种树的配额，分别记为Qi (i=1,2)。由于环境的承受能力，种植的树木总数不能超过给定的常数M，即Q1+Q2≤M并且假设M≥μ1+μ2。已知两种树的订购成本分别为cQi (i=1,2)。如果预留配额Qi小于种树申请数量Di，即Qi≤Di，则增加额外成本m[Di-Qi ]+ (i=1,2)。这里[x]+≜max⁡{x,0}.m,c,μi,σi为已知常数且满足关系(m-c)/c>(σ1/μ1 )2>(σ2/μ2 )2.蚂蚁森林希望选择种树配额Qi≥0(i=1,2)使得在最坏情况下总成本的期望极小，其中最坏情况是针对所有可能的均值为μi、方差为σi2的分布函数Fi。从数学上讲，目标是求解以下优化问题：,(1)subject to Q1+Q2≤M,Q1,Q2≥0其中Fi是所有均值为μi、方差为σi2 (i=1,2)的累积分布函数的集合，其支撑集为非负数。问题：请求解问题(1)，推导最优种树配额Qi,i=1,2的显式表达式。

进行一系列独立复生试验，每次成功概率为P，则在成功2次前失败3次的概率为。

设A,B为两事件，且P(A)=1/2,P(B)=1/3,P(A│B)=1/6，则P(A ̅│B ̅ )=【】

随机变量z ~ N(2,32)，则y=3z-2的数学期望为【】

甲袋中有2个红球3个白球，乙袋中也有2个红球3个白球，现从甲袋中任取2个球放入乙袋，然后再从乙袋中任取2个球。求最后取出的2个球全是白球的概率。

假设检验

设X1,X2,…,X16为来自总体N(μ,4)的简单随机样本.考虑假设检验问题：H0:μ≤10,H1:μ>10.Φ(x)表示标准正态分布函数，若该检验问题的拒绝域为W={X ̅≥11}，其中X ̅=1/16·Xi ，则μ=11.5时，该检验犯第二类错误的概率为【】

设某次考试的学生成绩服从正态分布，从中随机地抽取36位考生的成绩,算得平均成绩为66.5分，标准差为15分.问在显著性水平0.05下,是否可以认为这次考试全体考生的平均成绩为70分?并给出检验过程.附表：t分布表 P{t(n)≤tp (n)}=p

设x1,x2,⋯,xn为来自总体N(μ,2)的简单随机样本，记X ̅=1/n xi ,Zα表示标准正态分布的上侧α分位数，假设检验问题：H0:μ≤1,H1:μ>1的显著性水平为α的检验的拒绝域为【】