证 明 题(数学·2020年·山东省)
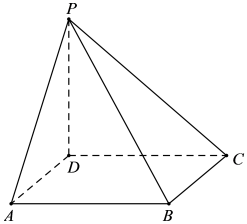
如图, 四棱锥 P − ABCD 的底面为正方形, PD ⊥ 底面 ABCD. 设平面 PAD 与平面 PBC 的交线为 l.
(1) 证明: l ⊥ 平面 P DC;
(2) 已知 PD = AD = 1, Q 为 l 上的点, 求 PB 与平面 QCD 所成角的正弦值的最大值.
解答提示
(1) 因为 PD⊥底面 ABCD, 所以 PD⊥AD.又底面 ABCD 为正方形, 所以 AD⊥DC. 因此 AD⊥平面 P DC.因为 AD // BC, AD ⊄ 平面 PBC, 所以 AD // 平面 PBC. 由已知得 l // AD.因此, l⊥平面 PDC.(2) 以 D 为坐标原点, 的方向为 x 轴正方向, 建立如图所示的空间直角坐标系 D − xyz. 则 D(0, 0, 0),C(0, 1, 0), B(1, 1...
查看完整答案,请下载word版
已知 A 为抛物线 C : y2 = 2px(p > 0) 上一点, 点 A 到 C 的焦点的距离为 12, 到 y 轴的距离为 9, 则 p=【 】。
设 a, b 为单位向量, 且 |a + b| = 1, 则 |a − b| =.
已知 F 为双曲线 C : =1 (a > 0, b > 0) 的右焦点, A 为 C 的右顶点, B 为 C 上的点, 且 BF垂直于 x 轴. 若 AB 的斜率为 3, 则 C 的离心率为 .
已椭圆 +y2 =1,圆x2 + y2=4,从圆上一点作椭圆的切点弦,求切点弦所围成的面积.
已知圆 x2 + y2 −6x = 0, 过点 (1,2) 的直线被该圆所截得的弦的长度的最小值为【 】
设 F1, F2 是双曲线 C : x2 −y2/3 = 1 的两个焦点, O 为坐标原点, 点 P 在 C 上且 |OP| = 2, 则 △PF1F2 的 面积为【 】
已知 A, B, C 为球 O 的球面上的三个点, ⊙O1 为 △ABC 的外接圆. 若 ⊙O1 的面积为 4π, AB = BC =AC = OO1,则球 O 的表面积为 【 】
已知 A, B, C 为球 O 的球面上的三个点, ⊙O1 为 △ABC 的外接圆. 若 ⊙O1 的面积为 4π, AB = BC = AC = OO1,则球 O 的表面积为【 】
如图是一个多面体的三视图, 这个多面体某条棱的一个端点在正视图中对应的点为 M, 在俯视图中对应的 点为 N, 则该端点在侧视图中对应的点为【 】
已知 △ABC 是面积为(9)/4 的等边三角形, 且其顶点都在球 O 的球面上, 若球 O 的表面积为 16π, 则 O到平面 ABC 的距离为【 】
已知直四棱柱 ABCD − A1B1C1D1 的棱长均为 2, ∠BAD = 60◦. 以 D1 为球心, 为半径的球面与侧面 BCC1B1 的交线长为.
某三棱柱的底面为正三角形, 其三视图如图所示, 该三棱柱的表面积为【 】
埃及胡夫金字塔是古代世界建筑奇迹之一, 它的形状可视为一个正四棱锥, 以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积, 则其侧面三角形底边上的高与底面正方形的边长的比值为 【】
如图, 在三棱锥 P − ABC 的平面展开图中, AC = 1, AB = AD = , AB ⊥ AC, AB ⊥ AD,cos ∠CAE = 30◦, 则 cos ∠FCB = .
已知圆锥的底面半径为 1, 母线长为 3, 则该圆锥内半径最大的球的体积为.
已知圆锥的侧面积 (单位: cm2) 为 2π, 且它的侧面展开图是一个半圆, 则这个圆锥的底面半径 (单位: cm) 为.
设三棱锥V-ABC中,∠AVB=∠BVC=∠CVA=直角.求证:ABC是锐角三角形.
已知圆锥体的底面半径为R,高为H.求内接于这个圆锥体并且体积最大的圆柱体的高h(如图).
如图,三棱锥P-ABC中,已知PA⊥BC,PA=BC=l,,PA,BC的公垂线,ED=h.求证:三棱锥P-ABC的体积V=l2h/6.

