证 明 题（数学·2020年·江苏省盐城市）

以下虚线框中为一个合作学习小组在一次数学实验中的过程记录，请阅读后完成虚线框下方的问题1~4.

(1)在Rt△ABC中，∠C=90°,AB=2，在探究三边关系时，通过画图，度量和计算，收集到，组数据如下表:(单位:厘米)

(2)根据学习函数的经验，选取上表中BC和AC+BC的数据进行分析；

①设BC=x,AC+BC=y，以(x,y)为坐标，在图①所示的坐标系中描出对应的点；

②连线；

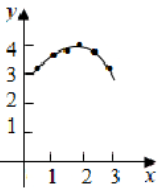
观察思考

(3)结合表中的数据以及所面的图像，猜想.当x=__________时，y最大；

(4)进一步C猜想:若Rt△MBC中，∠C=90°，斜边AB=2a(a为常数，a>0)，则BC= _________时，AC+BC最大.

推理证明

(5)对(4)中的猜想进行证明.

问题1.在图①中完善(2)的描点过程，并依次连线；

问题2.补全观察思考中的两个猜想:(3) _______ (4) _______

问题3.证明上述(5)中的猜想:

问题4.图②中折线B-E-F-G-A是一个感光元件的截面设计草图，其中点A,B间的距离是4厘米，AG=BE=1厘米，∠E=∠F=∠G=90°,平行光线从AB区域射入，∠BNE=60°,线段FM、FN为感光区城，当EF的长度为多少时，感光区域长度之和最大，并求出最大值.

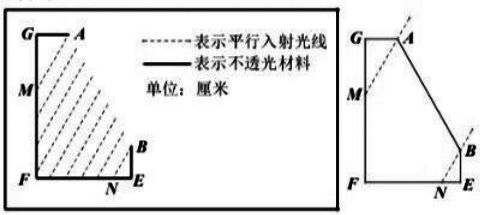
解答提示

问题1:图 问题2:(3)2(4)√2 a问题3:法一:(判别式法)证明:设BC=x,AC=BC=y在Rt△ABC中，∵∠C=90°,AC==,∴y=x+∴y-x=y2-2xy+x2=4a2-x2,2x2-2xy+y2-4a2=0,∵关于x的元二次方程有实根，∴b2-4ac=4y2-4×2⋅(x2-4a2 )≥0,∴y2≤8a2,∵y>0,a>0,∴y≤2 a,当y取最大值2√2 a时，2x2-4 ax+4a2=0( x-2a)2=0x1=x2=a∴当BC= a时，y有最大值.法二:(基本不等式)设BC=m,AC=n,AC+BC=y在Rt△ABC中，∵∠C=90°,∴m2+n2=4a2∵(m-n)2≥0, ∴m2+n2≥2mn.当m=n时，等式成立∴4a2≥2mn,mn≤2a2.∵y=m+n==，∵mn≤2a2,∴y≤2a,∴当BC=AC=a时，y有最大值.问题4:延长AM交EF于点C,过点A作AH⊥EF于点H,垂足为H,过点B作BK⊥GF交于点K,...

查看完整答案，请下载word版