单项选择（理工数学Ⅰ·2020年·全国统考）
设函数f(x,y)在点(0,0)处可微，f(0,0)=0,n= (∂f/∂x,∂f/∂y,-1)|(0,0)，非零向量r与n垂直，则【 】
A、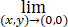
|n∙(x,y,f(x,y))|/
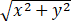存在
B、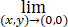|n×(x,y,f(x,y))|/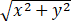存在
C、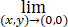|r∙(x,y,f(x,y))|/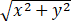存在
D、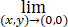|r×(x,y,f(x,y))|/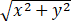存在
解答提示
A设f(x)在[0,+∞)上连续可导，f(0)=1，且对一切x≥0有|f(x)|≤e-x，求证：∃ξ∈(0,+∞)，使得f'(ξ)=e-ξ .
设实系数一元n次方程P(x)=a0xn+a1xn-1+…+an-1x+an (a0≠0，n≥2)的根全为实数，证明：方程P′(x)=0的根也全为实数.
设函数f(x)在[0,1]上二阶可导，且f(0)=0，f(1)=1，求证：存在ξ∈(0,1)，使得ξf″(ξ)+(1+ξ)f’(ξ)=1+ξ.
设函数f(x)在(-∞,+∞)上具有二阶导数，并且f″(x)>0，f′(x)=α>0，f′(x)=β<0，且存在一点x0使得f(x0)<0，证明：方程f(x)=0在(-∞,+∞)上恰有两个实根.
欧拉方程x2y″ + xy' - 4y = 0满足条件y(1) = 1,y'(1) = 2得解为y = .
有一圆柱体底面半径与高随时间变化的速率分别为2cm/s，-3cm/s，当底面半径为10cm，高为5cm时，圆柱体的体积与表面积随时间变化的速率分别为【 】
设函数f(x,y)可微，且f(x+1,ex)=x(x+1)2 , f(x,x2)=2x2lnx，则df(1,1)=【 】
设z=1/x·f(xy)+yf(x+y)，求∂2z)/∂x∂y.
已知f(x,y)在(x0,y0)的某邻域内，fx(x,y)连续，fy(x0,y0)存在，证明：f(x,y)在(x0,y0)可微.
若f(x,y)在区域D内对x和y都是连续的，则f(x,y)对(x,y)D为二元连续.
若f(x,y)的偏导数fx,fy在(x0,y0)存在，则f(x,y)在(x0,y0)连续.
设x(y),z(y)是由方程组所确定的隐函数，求x'(y),z'(y).