题吧，智能辅助学习中心
证 明 题（数学分析·2022年·华中科技大学）
证明：f(x)=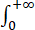
tx-1 e-t lntdt 在(0,+∞)上连续.
解答提示
记f(x)=tx-1 e-t lntdt +tx-1 e-t lntdt =I1+I2.对于I1,当0<x≤1时，tx-1 e-t lnt= lnt/t1-x =-∞，故t=0为瑕点.对∀[a,b]⊂(0,1],|tx-1 e-t lnt|≤-ta-1 e-t lnt取0<p=1-a/2<1，有-tp ta-1 e-t lnt=-ta/2 lnt=-=2/a ta/2 =0故-ta-1 e-t lntdt 收敛，由魏尔斯特拉斯判别法（M-判别法）知，I1在[a,b]上一致收敛，故在(0,1]内闭一致收敛....
查看完整答案，请下载word版
函数y=sinx|sinx|（其中|x|≤π/2）的反函数为.
设函数f(x)在(-∞,+∞)内有定义，对任意x都有f(x+1)=2f(x)，且当0≤x≤1时f(x)=x(1-x2)，试判断在x=0处函数f(x)是否可导.
设f(x)可导，F(x)=f(x)(1+|sinx|)，欲使F(x)在x=0可导，则必有【 】
设当x=0时，f(sinx)= f2(sinx)，f'(x)≠0，则f(0)=.
已知函数y=f(x)在x=2处连续，且=2求证f(x)在x=2处可导，并求f'(x)=2.
证明：两条心脏线ρ=α(1+cosθ)与ρ=α(1+cosθ)在交点处的切线相互垂直.
设y=y(x)由方程xef(y)=eyln29确定，其中具有二阶导数，f'≠1，则= .
设f(x)在[0,+∞)上连续可导，f(0)=1，且对一切x≥0有|f(x)|≤e-x，求证：∃ξ∈(0,+∞)，使得f'(ξ)=e-ξ .