证 明 题（数学分析·2022年·北京师范大学）
已知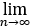
an=+∞，证明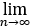(a1+a2+⋯+an)/n=+∞，并举例说明反过来不成立.
解答提示
已知an =+∞，则对∀M>0(不妨设M>2), ∃N1>0，当n≥N1时，有an>M.∴ (a1+a2+⋯+an)/n=(a1+a2+⋯+aN1))/n+(aN1+1+⋯+an)/n>(a1+a2+⋯+aN1)/n+((n-N1)M)/n.由于((n-N1)M)/n=M，则对于ε=1/M>0,∃N2>0,当n>N2时，M-ε<((n-N1 ))/n<M+ε，所以有((n-N1)M...
查看完整答案，请下载word版
已知函数f(x)是周期为π的奇函数，且当x∈（0，π/2）时f(x)=sinx-cosx+2，则当x∈（π，π/2）时f(x)=.
函数y=sinx|sinx|（其中|x|≤π/2）的反函数为.
证明：两条心脏线ρ=α(1+cosθ)与ρ=α(1+cosθ)在交点处的切线相互垂直.
设f(x)在[0,+∞)上连续可导，f(0)=1，且对一切x≥0有|f(x)|≤e-x，求证：∃ξ∈(0,+∞)，使得f'(ξ)=e-ξ .
设实系数一元n次方程P(x)=a0xn+a1xn-1+…+an-1x+an (a0≠0，n≥2)的根全为实数，证明：方程P′(x)=0的根也全为实数.
设函数f(x)在[0,1]上二阶可导，且f(0)=0，f(1)=1，求证：存在ξ∈(0,1)，使得ξf″(ξ)+(1+ξ)f’(ξ)=1+ξ.
设函数f(x)在(-∞,+∞)上具有二阶导数，并且f″(x)>0，f′(x)=α>0，f′(x)=β<0，且存在一点x0使得f(x0)<0，证明：方程f(x)=0在(-∞,+∞)上恰有两个实根.
设函数f(x)在(0,+∞)上连续可导，f(x)存在，f(x)的图形在(0,+∞)是上凸的，求证：f′(x)=0.