证 明 题（数学·2012年·广东省深圳市）

如图，在平面直角坐标系中，直线l：y=-2x+b(b≥0)的位置随b的不同取值而变化.

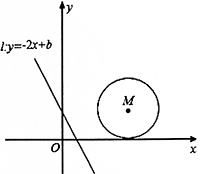
(1)已知⊙M的圆心坐标为(4,2),半径为2.

当b=______时，直线l：y=-2x+b(b≥0)经过圆心M；

当b=______时，直线l：y=-2x+b(b≥0)与⊙M相切；

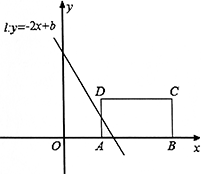
(2)若把⊙M换成矩形ABCD，其三个顶点坐标分别为：A(2,0)、B(6,0)、C(6,2).设直线l扫过矩形ABCD的面积为S，当b由小到大变化时，请求出S与b的函数关系式.

解答提示

(1)①直线l：y=-2x+b(b≥0)经过圆心M(4，2)时，则有：2=-2×4+b，∴b=10；②若直线l：y=-2x+b(b≥0)与⊙M相切，如图所示，应有两条符合条件的切线. 设直线与x轴、y轴交于A、B点，则A(b/2,0)、B(0,b)，∴OB=2OA.由题意，可知⊙M与x轴相切，设切点为D，连接MD；设直线与⊙M的一个切点为P，连接MP并延长交x轴于点G;过P点作PN⊥MD于点N，PH⊥x轴于点H.易证△PNN∽△BAO，∴PN:MN=OB:0A=2:1，∴PN=2MN.在Rt△PMN中，由勾股定理得：PM2=PN2+MN2，解得：MN=(2)/5,PN=(4)/5，∴PH=ND=MD-MN=2-(2)/5，OH=OD-HD=OD-PN=4-(4)/5，代入直线解析式求得：b=10-2；同理，当切线位于另外一侧时，可求得：b=10+2.(2) 由题意，可知矩形ABCD顶点D的坐标为(2，2).由一次函数的性质可知，当b由小到大变化时，直线l：2x+b(b≥0)向右平移，依次扫过矩形ABCD的不同部分.可得当直线经过A(2，0)时，b=4;当直线经过D(2，2)时，b=6；当直线经过B(6，0...

查看完整答案，请下载word版