证 明 题（数学·2021年5月·阿里巴巴）

当某公司推出一个新的社交软件时，公司的市场部门除了会关心该软件的活跃客的总人数随时间的变化，也会对客户群体的一些特征做具体的调研和分析。我们用n(t,x)表示客户的数量密度(以下简称密度)，这里t表示时间，而x表示客户对该社交软件的使用时长，那么在t时刻，对于0<x₁<x₂，使用时长介于x₁和x₂之间的客户数量为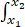n(t,x)dx。我们假设，密度n(t,x)随着时间演化受以下几个因素的影响：

假设1.当客户持续使用该社交软件时,他的使用时长随时间线性增长。

假设2.客户在使用过程中，可能会停止使用，我们假设停止速率d(x)>0只跟使用时长x有关。

假设3.新客户的来源有两个。

①公司的宣传：单位时间内因此增加的人数是时间的函数，用c(t)表示。

②老客户的宣传：老客户会主动向自己的同事、朋友等推荐使用该社交软件，推荐成功的速率跟客户的使用时长x有关，记作b(x)。

假设如果在某一时刻，记为t=0时，密度函数是已知的，n(0,x)=n₀ (x)。可以推导出，n(t,x)的时间演化满足如下的方程

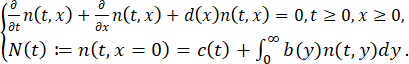    (1)

这里N(t)可解读为新客户的增加速率。我们假设b,d∈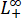(0,∞)，即b(x)和d(x)正且(本质)有界。以下,我们先做一个简化假设：c(t)≡0，即新客户的增加只跟老客户的宣传有关。

(i)问答题(10分)根据假设1和假设2，形式地推导出(1)中n(t,x)所满足的偏微分方程，需要在推导过程中指出模型假设和数学表达式之间的对应关系。再根据假设3，解释(1)中N(t)的定义的含义。

(ii)问答题(10分)我们想要研究新客户的增加速率N(t)和推荐成功速率b(x)之间的关系。为此,请推导出一个N(t)所满足的方程，且方程中只包含N(t),n₀ (x),b(x),d(x)，而不包含n(t,x)。并证明，N(t)满足如下估计

|N(t)|≤‖b‖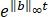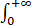_∞|n₀ (x)|dx,

这里‖∙‖_∞表示L^∞范数。

(iii)证明题(10分)最后，我们想要研究，在充分长的时间之后，数量密度函数n(t,x)有什么渐近的趋势。由于客户总人数可能一直在增加，所以我们不方便直接研究数量密度函数n(t,x)，而更应该去看一个重整化的密度函数。

为此，我们首先假设如下的特征值问题有唯一解(λ₀,φ(x))：

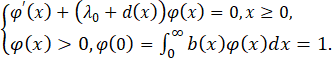
并且它的对偶问题也有唯一的解ψ(x)：

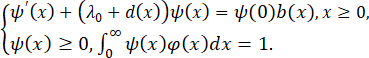
然后，我们定义重整化密度n ̃(t,x)≔n(t,x)e^{-λ0 t}。证明，对于任意凸函数H:R⁺→R⁺满足H(0)=0，我们有

d/dt 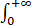ψ(x)φ(x)H(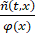)dx≤0,∀t≥0,

并证明

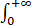ψ(x)n(t,x))dx=e^λ0t 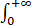ψ(x) n₀ (x)dx.

解答提示

(i)这个方程推导方式有很多。举两个例子。1.特征线法。由于使用时长随时间线性增长，我们定义特征线x(t)，它满足=1.而顺着特征线，根据停止速率的含义，我们有n(t,x(t))=-d(x(t))n(t,x(t)).整理即得(1)式方程。2.微元法。考虑一个时间微元δt≪1，根据假设1和假设2，我们有n(t+δt,x+δt)=n(t,x)-δtd(x)n(x,t)+o(δt).其中右端第一项表示时间平移的贡献，第二项表示停止的客户数量。两边除以δt,再令δt→0，即得此方程。关于N(t)的定义，只需要说明老客户推荐的贡献。对于固定某个使用时长x的老客户，他们单位时间内介绍的新客户的数量b(x)n(t,x)。为了求单位时间内所有老客户介绍的新客户数量，需要把所有使用时长的老客户的贡献加在一起，故表达为b(y)n(t,y)dy。(ii)根据题意和N(t)的定义,我们需要先把密度函数n(t,x)写成N(t)和其他参数的表达式，这需要求解此方程。注意到这是一个一阶双曲方程，可以用特征线法求解。将方程改写为 n(t+s,x+s)+d(x+s)n(t+s,x+s)=0,则如果定义D(x)=d(y)dy，那么[eD(x+s) n(t+s,x+s)]=0.那么，当s≥max⁡(-t,-x)时，我们有eD(x+s) n(t+s,x+s)=eD(x) n(t,x),∀x≥0,t≥0.特别的，我们可以令x=y,s=-y可得，当t≥y时n(t,y)=N(t-y) e-D(y) .再令x=y,s=-t可得，当t≤y时n(t,y)=n0 (y-t) eD(y-t)-D(y).为了导出N(t)满足的方程，我们将它的表达式拆分成两部分N(t)=b(y)n(t,y)dy=b(y)n(t,y)dy+b(y)n(t,y)dy.根据特征线可知，右端第一项的特征...

查看完整答案，请下载word版