证 明 题（数学·2020年11月·中国数学奥林匹克）
已知正整数n,恰有36个不同的质数整除n，对k=1,2,3,4,5，记[(k-1)n/5,kn/5]中互质的整数个数为Cn，已知C1,C2,C3,C4,C5不完全相同.
求证：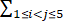
(Ci - Cj)2 ≥236.
解答提示
不妨设n=p1 p2…p36.定义f(n)=([n/5],[2n/5]-[n/5],[3n/5]-[2n/5],[4n/5]-[3n/5],[5n/5]-[4n/5])，若n=0，则f(0)=(0,0,0,0,0)，可忽略.约定∀k∈R (a1+k,a2+k,a3+k,a4+k,a5+k)=(a1,a2,a3,a4,a5 )所以，若a≡b(mod5),则f(a)=f(b)设A=(c1,c2,c3,c4,c5 )=f(n)-[(f(n/p1 )+f(n/p2 )+⋯)]+[(f(n/(p1 p2 ))+⋯)]若n不为5的倍数，设n≡,1/pi ≡ (mod 5)，定义g(x)=f(2x)，则g(x+4)=g(x).则A=g(a0 )-[g(a0+a1 )+g(a0+a2 )+⋯]+[g(a0+a1+a2 )+⋯]取h(x)= (-1)(-1)…(-1)=(x-1)d (x2-1)e (x3-1)f (x4-1)g=-(++⋯)+(+⋯) 于是A中g(t)(t=1,2,3,4)的个数为a0,a0+a1,a0+a2,…中≡(mod 4)的个数，[注：①g(4k+t)视为g(t);② 若a0+ai≡t(mod 4),视作“-1”个”“ ≡t(mod ...
查看完整答案，请下载word版
设集合 A ={x | x2 −4 ⩽ 0},B ={x | 2x + a ⩽ 0}, 且 A∩B ={x |−2 ⩽ x ⩽ 1}, 则 a =【】
埃及胡夫金字塔是古代世界建筑奇迹之一, 它的形状可视为一个正四棱锥, 以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积, 则其侧面三角形底边上的高与底面正方形的边长的比值为 【】
已知 A 为抛物线 C : y2 = 2px(p > 0) 上一点, 点 A 到 C 的焦点的距离为 12, 到 y 轴的距离为 9, 则 p=【 】。
已知 A, B, C 为球 O 的球面上的三个点， ⊙O1 为 △ABC 的外接圆. 若 ⊙O1 的面积为 4π， AB = BC =AC = OO1，则球 O 的表面积为 【 】
设 a, b 为单位向量, 且 |a + b| = 1, 则 |a − b| =.
已知 F 为双曲线 C : =1 (a > 0, b > 0) 的右焦点, A 为 C 的右顶点, B 为 C 上的点, 且 BF垂直于 x 轴. 若 AB 的斜率为 3, 则 C 的离心率为 .
函数 f(x) = x4 − 2x3 的图像在点 (1, f(1)) 处的切线方程为【 】。
设函数 f(x) = cos (ωx + π/6 ) 在 [−π, π] 的图像大致如下图, 则 f(x) 的最小正周期为【 】。
已知 α ∈ (0, π), 且 3cos2α − 8cosα = 5, 则 sinα =【 】
若 2a + log2a = 4b + 2log4b, 则【 】
若 x, y 满足约束条件 则 z = x + 7y 的最大值为 .
设 {an} 是公比不为 1 的等比数列, a1 为 a2, a3 的等差中项.(1) 求 {an} 的公比;(2) 若 a1 = 1, 求数列 {nan} 的前 n 项和.
已知函数 f(x) = ex + ax2 − x.(1) 当 a = 1 时, 讨论 f(x) 的单调性;(2) 当 x ⩾ 0 时, f(x) ⩾ x3 + 1, 求 a 的取值范围.
已知函数 f(x) = |3x + 1| − 2|x − 1|.(1) 画出 y = f(x) 的图像;(2) 求不等式 f(x) > f(x + 1) 的解集.