2022年山东省青岛市初中学业水平考试(中考)数学试卷

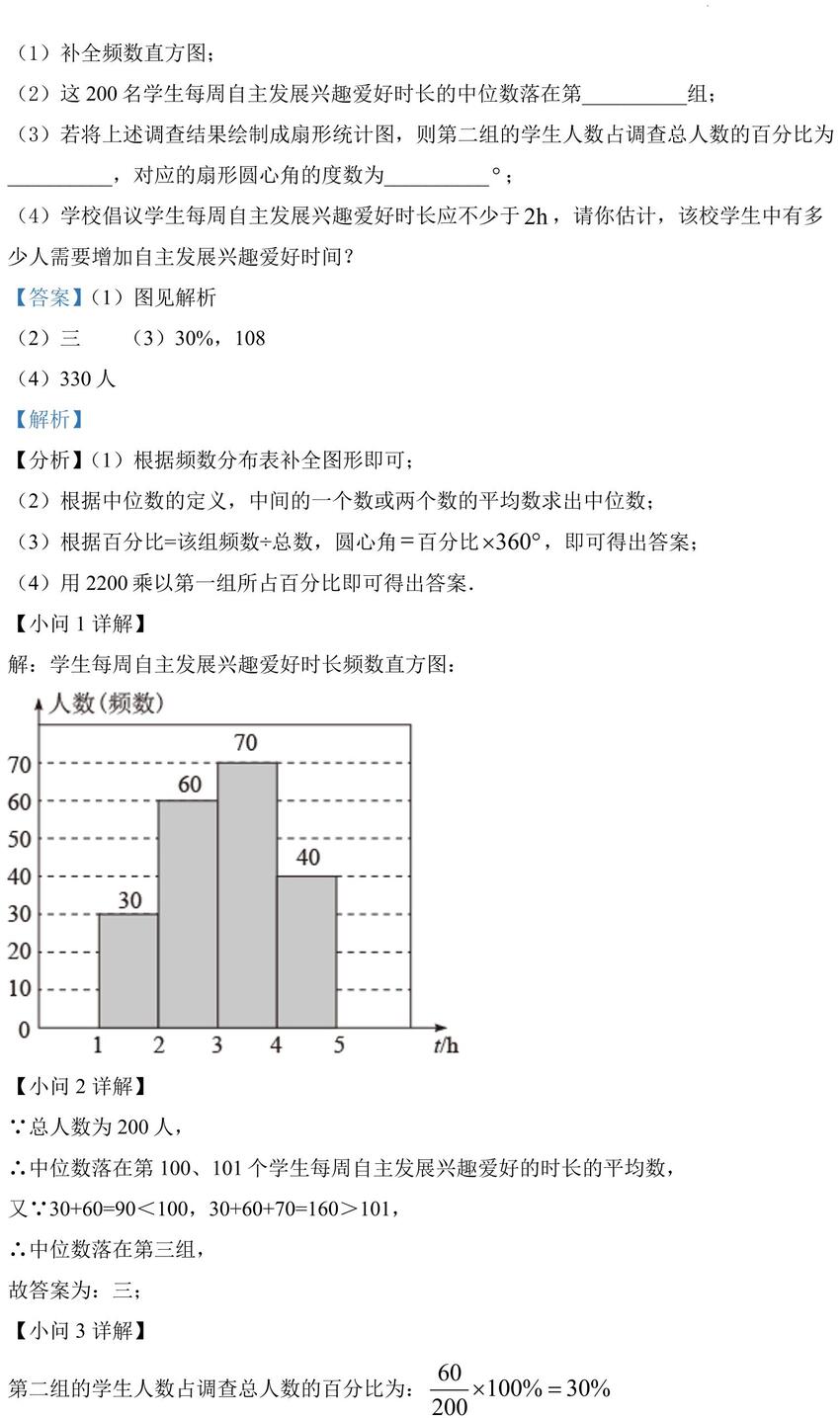
（1）补全频数直方图；

（2）这 200 名学生每周自主发展兴趣爱好时长的中位数落在第__________组；

（3）若将上述调查结果绘制成扇形统计图，则第二组的学生人数占调查总人数的百分比为

__________，对应的扇形圆心角的度数为__________ ；

（4）学校倡议学生每周自主发展兴趣爱好时长应不少于 ，请你估计，该校学生中有多少人需要增加自主发展兴趣爱好时间？

【答案】（1）图见解析

（2）三 （3）30%，108

（4）330人

【分析】（1）根据频数分布表补全图形即可；

（2）根据中位数的定义，中间的一个数或两个数的平均数求出中位数；

（3）根据百分比=该组频数÷总数，圆心角 百分比 ，即可得出答案；

（4）用 2200乘以第一组所占百分比即可得出答案．

【小问 1详解】 解：学生每周自主发展兴趣爱好时长频数直方图：

【小问 2详解】

∵总人数为 200人，

∴中位数落在第 100、101 个学生每周自主发展兴趣爱好的时长的平均数， 又∵30+60=90＜100，30+60+70=160＞101，

∴中位数落在第三组， 故答案为：三；

【小问 3详解】 第二组的学生人数占调查总人数的百分比为：