单项选择（数学·2018年·广东省深圳市）

如图，A,B是函数y=12/x上两点，P为一动点，作PY//y轴，PA//x轴，下列说法正确的是【 】

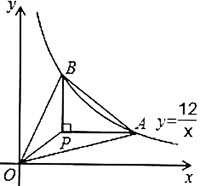
①△AOP≅△BOP；②S_△AOP=S_△BOP；

③若OA=OB，则OP平分∠AOB；

④若S_△BOP=4，则S_△ABP=16.

A、①③

B、②③

C、②④

D、③④

解答提示

B∵点P是动点，∴AP与BP不一定相等，故△AOP与△BOP不一定全等，①不正确；设P(m,n)，∵PB//y轴，∴B(m,12/m),BP=|12/m-n|,∴S△BOP=1/2 |12/m-n|×m=1/2 |12-mn|.∵PA//x轴，∴A(12/n,n),AP=|12/n-m|,∴S△AOP=1/2 |12/n-m|×n=1/2 |12-mn|.∴S△AOP=S△BOP,②正确；如图，作PE⊥OB于E,PF⊥OA于F，则S△AOP=1/2 OA×PF,S△BOP=1/2 OB×PE,∵S△AOP=S...

查看完整答案，请下载word版