证 明 题（数学分析·2022年·华中科技大学）

已知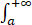f(x)dx条件收敛，且

f⁺(x)=(|f(x)|+f(x))/2,f^-(x)=(|f(x)|-f(x))/2

证明：(1) 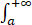f⁺(x)dx,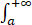f^-(x)dx均发散到+∞;

(2)当A→+∞时，f⁺(x) dx与f^-(x)dx等价.

解答提示

(1)由条件知：f(x)=f+ (x)-f- (x),|f(x)|=f+ (x)+f- (x),整理得：|f(x)|=2f+ (x)-(f+ (x)-f- (x))=2f+ (x)-f(x).假如f+ (x) dx收敛，又由已知f(x) dx也收敛，故|f(x)| dx收敛，也已知f(x) dx条件收敛矛盾，所以f+ (x) dx发散到+∞.同样，由已条件可得：...

查看完整答案，请下载word版