计 算 题（数学分析·2022年·同济大学）

计算积分∬_SzdS，其中S为曲面x²+z²=2az(a>0)被曲面z=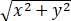所截的部分.

解答提示

由对称性，只需计算第一卦限部分.将第一卦限部分在yOz平面作投影Dyz:z=a,z=2a,y=0,2z2=2az+y2.由曲面方程得x=,∴∂x/∂y=0,∂x/∂z=(a-z)/,∴√(1+(∂x/∂y)2+(∂x/∂z)2 )=a/.∴1/4 ∬Sz dS=∬Dyzz a/ dydz=adzz/ dy=√2 az dz令t=，上式=√2 a((2at2+a)2at2)/(1+t2 )3 dt=4√2 a3 t4/(1+t2 )3 dt+2√2 a3 t2/(1+t2 )3 dtt4/(1+t2 )3 dt=[1/(t2+1)-2/(t2+1)2 +1/(t2+1)3 ] dt=1/(t2+1) dt-21/(1+t2 )2 dt+1/(1+t2 )3 dt= arctant|0+∞-21/(1+t2 )2 dt+3/4 1/...

查看完整答案，请下载word版