证 明 题（数学·2022年·全国甲·文）
在直角坐标系xOy中，曲线C1的参数方程为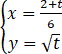
，（t为参数），曲线C2的参数方程为
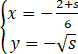，（s为参数）.
（1）写出C1的普通方程；
（2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，曲线C3的极坐标方程为2cosθ-sinθ=0，求C3与C1交点的直角坐标，及C3与C2交点的直角坐标.
解答提示
（1）由，（t为参数），消去参数t可得C1的普通方程为y2=6x-2(y≥0)；（2）由，（s为参数），消去参数s可得C2的普通方程为y2=-6x-2(y≤0).由2cosθ-sinθ=0得2ρcosθ-ρsinθ=0，所以曲线C3...
查看完整答案，请下载word版
函数 f(x) = x4 − 2x3 的图像在点 (1, f(1)) 处的切线方程为【 】。
设函数 f(x) = cos (ωx + π/6 ) 在 [−π, π] 的图像大致如下图, 则 f(x) 的最小正周期为【 】。
已知 α ∈ (0, π), 且 3cos2α − 8cosα = 5, 则 sinα =【 】
若 2a + log2a = 4b + 2log4b, 则【 】
设 {an} 是公比不为 1 的等比数列, a1 为 a2, a3 的等差中项.(1) 求 {an} 的公比;(2) 若 a1 = 1, 求数列 {nan} 的前 n 项和.
已知函数 f(x) = ex + ax2 − x.(1) 当 a = 1 时, 讨论 f(x) 的单调性;(2) 当 x ⩾ 0 时, f(x) ⩾ x3 + 1, 求 a 的取值范围.
已知函数 f(x) = |3x + 1| − 2|x − 1|.(1) 画出 y = f(x) 的图像;(2) 求不等式 f(x) > f(x + 1) 的解集.
正实数x,y,z,w满足x≥y≥w，且x+y≤2(w+z)，求 + 的最小值.
已知x,y,z>0，判断s=x/(x+y) + y/(y+z) + z/(z+x) 是否存在最大值与最小值.
已知数列{an}满足：a1=1，a2=4,且an2 - an-1an+1=2n-1(n≥2,n∈N*)，求a2020的个位数.
若 x, y 满足约束条件 则 z = x + 7y 的最大值为 .
若f(x)=x5+px+q有有理根，且正整数p,q不大于100，则满足条件的(p,q)共有几组.
若 x, y 满足约束条件 , 则 z = x + 2y 的最大值是.
若 x, y 满足约束条件, 则 z = 3x + 2y 的最大值是.
已知函数 f(x) =.若函数 g(x) = f(x) − |kx2 − 2x| (k ∈ R) 恰有 4 个零点, 则 k 的取值范围 是【 】.
若x0是方程(1/2 )x=x1/3的解，则x0属于区间【 】