证 明 题（数学·2021年·江苏省苏州市）

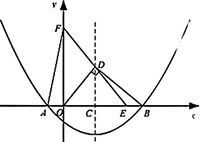
如图，二次两数y=x²-(m+1)x+m(m是实数，且-1<m<0)的图像与x轴交于A,B两点(点A在点B的左侧)，其对称轴与x轴交于C.已知点D位于第一象限，且在对称轴上，OD⊥BD，点E在x轴的正半轴上，OC=EC，连接ED并延长交y轴于点F，连接AF.

(1)求A,B,C三点的坐标(用数字或含m的式子表示)；

(2)已知点Q在拋物线的对称轴上，当△AFQ的周长的最小值等于12/5时，求m的值.

解答提示

(1)由x2-(m+1)x+m=0得x=m或x=1,∴A(m,0),B(1,0)，∴对称轴为直线x=(m+1)/2,∴C((m+1)/2,0).(2)在Rt△ODB中，CD⊥OB,OC=(m+1)/2,BC=1-(m+1)/2=(1-m)/2.由△COD∼△CBD，得CD2=OC∙CB=(m+1)/2∙(1-m)/2=(1-m2)/2.∵CD⊥x轴，OF⊥x轴，且OC=EC，∴OF=2CD,OF2...

查看完整答案，请下载word版