2020年辽宁省中考试题-代数-函数-二次函数

证明题（数学·2020年·辽宁省）

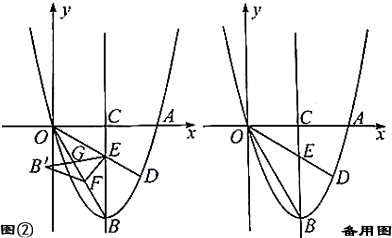
如图，抛物线y=ax²-2x+c（a≠0）过点O(0,0)和A(6,0)，点B是抛物线的顶点，点D是x轴下方抛物线上的一点，连接OB，OD.

（1）求抛物线的解析式；

（2）如图①，当∠BOD=30°时，求点D的坐标；

（3）如图②，在（2）的条件下，抛物线的对称轴交x轴于点C，交线段OD于点E，点F是线段OB上的动点（点F不与点O和点B重合，连接EF，将ΔBEF沿EF折叠，点B的对应点为点B，ΔEFB'与ΔOBE的重叠部分为ΔEFG，在坐标平面内是否存在一点H，使以点E，F，G，H为顶点的四边形是矩形？若存在，请直接写出点H的坐标，若不存在，请说明理由.

解答提示

（1）把点O(0,0)和A(6,0)分别代入y=ax2-2 x+c中，得解得∴抛物线的解析式为y=/3 x2-2 x.（2）如图，设抛物线的对称轴与x轴相交于点M，与OD相交于点N∵y=/3 x2-2 x=/3(x-3)2-3∴顶点B(3,-3)，对称轴与x轴的交点M(3,0)∴OM=3，MB=3∵在Rt ΔOMB中，tan⁡∠ MOB=BM/OM=(3)/3=∴∠MOB=60°∵∠BOD=30°∴∠MOD=∠MOB-∠BOD=60°-3...

查看完整答案，请下载word版

代数

下列运算正确的是【】

不等式组的解集是【】

如图是一组有规律的图案，它们是由边长相等的正三角形组合而成，第1个图案有4个三角形，第2个图案有7个三角形，第3个图案有10个三角形⋯按此规律摆下去，第n个图案有个三角形（用含n的代数式表示）．，，，，…

下面是小彬同学进行分式化简的过程，请认真阅读并完成相应任务．= 第一步= 第二步= 第三步= 第四步= 第五步= 第六步任务一：填空：①以上化简步骤中，第步是进行分式的通分，通分的依据是或填为；②第步开始出现错误，这一步错误的原因是；任务二：请直接写出该分式化简后的正确结果；任务三：除纠正上述错误外，请你根据平时的学习经验，就分式化简时还需要注意的事项给其他同学提一条建议．

2020年5月份，省城太原开展了“活力太原·乐购晋阳”消费暖心活动，本次活动中的家电消费券单笔交易满600元立减128元（每次只能使用一张）某品牌电饭煲按进价提高50%后标价，若按标价的八折销售，某顾客购买该电饭煲时，使用一张家电消费券后，又付现金568元．求该电饭煲的进价．

若关于x的不等式3x+a≤2只有2个正整数解，则a的取值范围为【】

观察等式： 2+22=23-2；2+22+23=24-2；2+22+23+24=25-2；…已知按一定规律排列的一组数：2100，2101，2102，…，2199，2200若2100=S，用含S的式子表示这组数据的和是【】

分解因式：m3n - mn=.

一个三角形的两边长分别为2和5，第三边长是方程x2-8x+12=0的根，则该三角形的周长为.

已知a+2b=10/3，3a+4b=16/3，则a+b的值为.

函数

已知点A(x1,y1 )，B(x2,y2 )，C(x3,y3 )都在反比例函数y=k/x (k<0)的图像上，且x1<x2<0<x3，则y1，y2，y3的大小关系是【】

已知函数y=，则自变量x的取值范围是.

如图所示，一次函数y=mx+n(m≠0)的图象与反比例函数y=k/x (k≠0)的图象交于第二、四象限的点A(-2,a)和点B(b,-1)，过A点作x轴的垂线，垂足为点C，ΔAOC的面积为4. （1）分别求出a和b的值；（2）结合图象直接写出mx+n>k/x中x的取值范围；（3）在y轴上取点P，使PB-PA取得最大值时，求出点P的坐标.

已知y=-x+5，当x分别取1，2，3，……，2020时，所对应y值的总和是.

通过课本上对函数的学习，我们积累了一定的经验.下表是一个函数的自变量x与函数值y的部分对应值，请你借鉴以往学习函数的经验，探究下列问题：x … 0 1 2 3 4 5 …y … 6 3 2 1.5 1.2 1 … （1）当x=时，y=1.5；（2）根据表中数值描点(x,y)，并画出函数图象；（3）观察画出的图象，写出这个函数的一条性质：.

如图，点A是反比例函数y=3/x图象上任意一点，过点A分别作x轴，y轴的垂线，垂足为B，C，则四边形OBAC的面积为．

如图，一次函数y=x+1的图象与反比例函数y=k/x的图象相交，其中一个交点的横坐标是2．（1）求反比例函数的表达式；（2）将一次函数y=x+1的图象向下平移2个单位，求平移后的图象与反比例函数y=k/x图象的交点坐标；（3）直接写出一个一次函数，使其过点(0,5)，且与反比例函数y=k/x的图象没有公共点．

第33个国际禁毒日到来之际，贵阳市策划了以“健康人生，绿色无毒”为主题的禁毒宣传月活动，某班开展了此项活动的知识竞赛．学习委员为班级购买奖品后与生活委员对话如下：（1）请用方程的知识帮助学习委员计算一下，为什么说学习委员搞错了；（2）学习委员连忙拿出发票，发现的确错了，因为他还买了一本笔记本，但笔记本的单价已模糊不清，只能辨认出单价是小于10元的整数，那么笔记本的单价可能是多少元？

把1-9这9个数填入3×3方格中，使其任意一行，任意一列及两条对角线上的数之和都相等，这样便构成了一个“九宫格”.它源于我国古代的“洛書”(图①)，是世界上最早的“幻方”.图②是仅可以看到部分数值的“九宫格”，则其中x的值为【】

若二次函数y=ax2+bx+c的图像与x轴有两个交点M(x1,0),N(x2,0)(0<x1<x2 )，且经过点A(0,2),过点A的直线l与x轴交于点C,与该函数的图像交于点B (异于点A).满足△ACN是等腰直角三角形，记△AMN的面积为S1,△BMN的面积为S2，且S2=5/21.(1)抛物线的开口方向(填“上”或“下”)；(2)求直线l相应的函数表达式；(3)求该二次函数的表达式.

二次函数

竖直上抛物体离地面的高度h(m)与运动时间t(s)之间的关系可以近似地用公式h=-5t2+v0t+h0表示，其中h0 (m)是物体抛出时离地面的高度，v0 (m/s)是物体抛出时的速度．某人将一个小球从距地面1.5m的高处以20m/s的速度竖直向上抛出，小球达到的离地面的最大高度为【】

如图，抛物线y=x2-x-3与x轴交于A，B两点（点A在点B的左侧），与y轴交于点C．直线l与抛物线交于A，D两点，与y轴交于点E，点D的坐标为(4,-3)．（1）请直接写出A，B两点的坐标及直线l的函数表达式；（2）若点P是抛物线上的点，点P的横坐标为 (m≥0)，过点P作PM⊥x轴，垂足为M．PM与直线l交于点N，当点N是线段PM的三等分点时，求点P的坐标；（3）若点Q是y轴上的点，且∠ADQ=45°，求点Q的坐标．

若函数y=ax2+bx+c(a≠0)的图象如图所示，则函数y=ax+b和y=c/x在同一平面直角坐标系中的图象大致是【】

如图所示，抛物线y=ax2+bx+c(a≠0)与x轴交于A、B两点，与y轴交于点C，且点A的坐标为A(-2,0)，点C的坐标为C(0,6)，对称轴为直线x=1.点D是抛物线上一个动点，设点D的横坐标为m(1<m<4)，连接AC，BC，DC，DB. （1）求抛物线的函数表达式；（2）当ΔBCD的面积等于ΔAOC的面积的3/4时，求m的值；（3）在（2）的条件下，若点M是x轴上一动点，点N是抛物线上一动点，试判断是否存在这样的点M，使得以点B,D,M,N为顶点的四边形是平行四边形.若存在，请直接写出点M的坐标；若不存在，请说明理由.

如图，在平面直角坐标系中，抛物线y=ax2+bx-2交x轴于A，B两点，交y轴于点C，且OA=2OC=8OB.点P是第三象限内抛物线上的一动点. （1）求此抛物线的表达式；（2）若PC//AB，求点P的坐标；（3）连接AC，求ΔPAC面积的最大值及此时点P的坐标.

把函数y=(x-1)2+2的图象向右平移1个单位长度，平移后图象的函数解析式为【】

如图，抛物线y=ax2+bx+c的对称轴是x=1.下列结论： abc>0；②b2-4ac>0；③8a+c 正确的有【】

如图，抛物线y= x2+bx+c与x轴交于A，B两点，点A，B分别位于原点的左、右两侧，BO=3AO=3，过点B的直线与y轴正半轴和抛物线的交点分别为C，D，BC=CD. (3+)/6（1）求b，c的值；（2）求直线BD的函数解析式；（3）点P在抛物线的对称轴上且在x轴下方，点Q在射线BA上，当ΔABD与ΔBPQ相似时，请直接写出所有满足条件的点Q的坐标.

已知二次函数y=ax2+bx+c的图象经过(-3,0)与(1,0)两点，关于x的方程ax2+bx+c+m=0 (m>0)有两个根，其中一个根是3．则关于x的方程ax2+bx+c+n (0<n<m)有两个整数根，这两个整数根是【】

2020年体育中考，增设了考生进入考点需进行体温检测的要求．防疫部门为了解学生错峰进入考点进行体温检测的情况，调查了一所学校某天上午考生进入考点的累计人数y（人）与时间x（分钟）的变化情况，数据如下表：（表中9~15表示9<x≤15）（1）根据这15分钟内考生进入考点的累计人数与时间的变化规律，利用初中所学函数知识求出y与x之间的函数关系式；（2）如果考生一进考点就开始测量体温，体温检测点有2个，每个检测点每分钟检测20人，考生排队测量体温，求排队人数最多时有多少人？全部考生都完成体温检测需要多少时间？（3）在（2）的条件下，如果要在12分钟内让全部考生完成体温检测，从一开始就应该至少增加几个检测点？