高考题1984年全国统考( )
设a>2,给定数列{xn},其中x1 = a,xn+1=(xn2)/(2(xn-1)) (n=1,2,…),求证:
(1) xn>2,且xn+1/xn < 1(n=1,2,…);
(2) 如果a≤3,那么xn ≤ 2+1/2n-1 (n=1,2,…);
(3) 如果a>3,那么当n ≥ (lga/3)/(lg4/3)时,必有xn+1<3.
(1) 先证明xn>2(n=1,2,…).用数学归纳法.
由条件a>2及x1=a知不等式当n=1时成立.
假设不等式当n=k(k≥1)时成立.
当n=k+1时,因为由条件及归纳假设知
xk+1>2⇔xk2-4xk+4>0⇔(xk-2)2>0,
再由归纳假设知不等式(xk-2)2>0成立.
从而不等式xn>2对所有的正整数n成立.
也可以这样证:
由已知条件, xk+1=1/2 [(xk-1)+1/(xk-1)+2]>1/2 (2+2)=2.
所以不等式xn>2(n=1,2,…)成立.
再证明xn+1/xn <1(n=1,2,…).
由条件xn>2(n=1,2,…)知
xn+1/xn <1⇔xn/(2(xn-1))<1⇔xn>2.
因此不等式xn+1/xn <1(n=1,2,…)也成立.
(2) 用数学归纳法.
由条件x1=a≤3知不等式当n=1时成立.
假设不等式当n=k(k≥1)时成立.
当n=k+1时,由条件及xk>2知
xk+1≤2+1/2k ⇔xk2≤2(xk-1)(2+1/2k )
⇔xk2-2(2+1/2k ) xk+2(2+1/2k )≤0
⇔(xk-2)[xk-(2+1/2k-1 )]-1/2k-1 ≤0
再由xk>2及归纳假设知,上面最后一个不等式一定成立,所以不等式xk+1≤2+1/2k 也成立.
从而不等式xn≤2+1/2n-1 (n=1,2,…)成立.
(3) 先证明若xk>3,则xk+1/xk <3/4.
这是因为xk+1/xk =1/2 (1+1/(xk-1))<1/2 [1+1/(3-1)]=3/4.
然后用反证法.
若当n≥(lga/3)/(lg4/3)时,有xn+1≥3,则由第(1)小题知
x1>x2>⋯>xn>xn+1≥3.
因此,由上面证明的结论及x1=a可得
3≤xn+1=x1∙x2/x1 ∙x3/x2 ∙⋯∙xn+1/xn <a(3/4)n,
即n<(lga/3)/(lg4/3),这与假设矛盾,所以本小题的结论成立.
高考题1981年全国统考( )
用数学归纳法证明等式
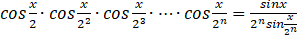
对一切自然数n都成立.
(i)当n=1时,左边=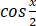 ,
,
而右边=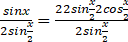 =
= ,
,
所以n=1时等式成立.
(ii)假设当n=k时等式成立,即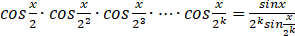 ,
,
两边同乘以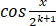 ,得
,得

=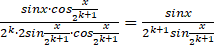 ,
,
所以当n=k+1时等式也成立.
根据(i)和(ii),就证明了对一切自然数n等式都成立.

